Визначення невласного інтегралу І роду

Лекція 37. Невласні інтеграли І роду

План

Визначення невласного інтегралу І роду

Визначення 1. Нехай функція 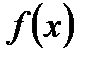визначена на 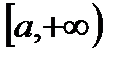. Припустимо, що 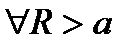існує 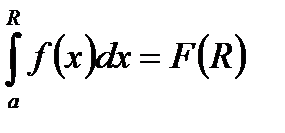. Невласним інтегралом (НІ) I роду називається

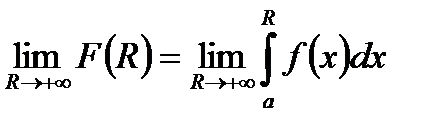, (1)

Якщо границя (1) існує, то кажуть, що НІ збігається, інакше – розбігається.

Зауваження. Якщ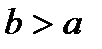о , то

і інтеграли 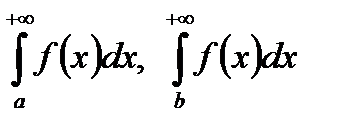збігається і розбігаються одночасно. Дійсно

Приклад. Обчислити чи довести розбіжність інтеграла .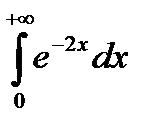

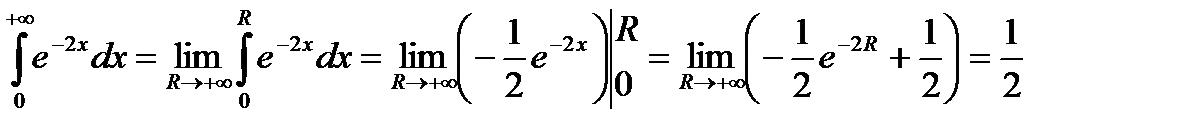Таким чином, поданий інтеграл збігається і дорівнює ½.

Дата добавления: 2015-08-21; просмотров: 590;