Критерій Коші збіжності невласного інтегралу І роду

При вивченні властивостей функції однієї змінної було встановлено, що для того, щоб 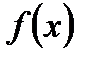мала границю в точці 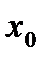необхідно і достатньо, щоб вона задовольняла умові Коші в цій точці, тобто щоб

для 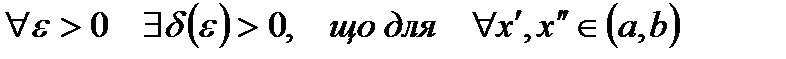таких, що 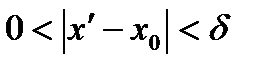, , 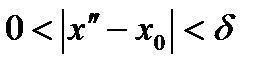виконується нерівність:

.

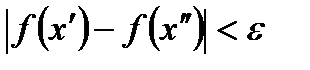Збіжність НІ І роду еквівалентна існуванню границі (1) функції одної змінної 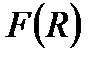. Таким чином:

якщо для 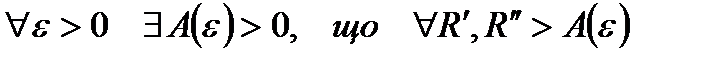виконується нерівність

,

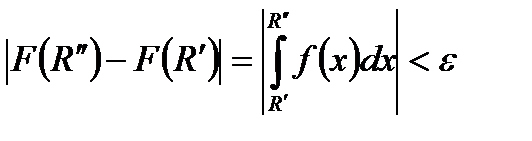то границя (1) існує. Таким чином, ми довели наступну теорему.

Теорема 1 (Критерій Коші збіжності невласного інтегралу І роду). Для того, щоб збігався невластивий інтеграл I роду необхідно і достатньо щоб

: .

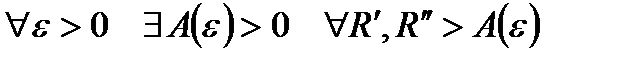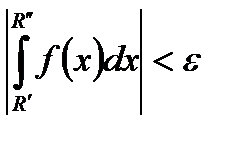3.Загальна достатня умова збіжності невласного інтегралу І роду

Теорема 2. Нехай функції 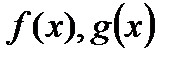визначені на 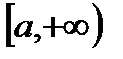і виконуються наступні умови:

1) , ;

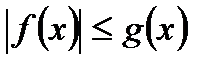2) 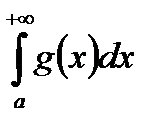- збігається,

то збігається і .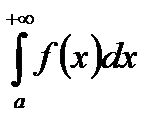

Доказ. Іх збіжності інтегралу 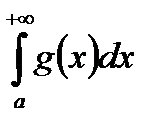за критерієм Коші (теорема 1) витікає, що

.

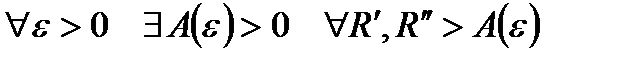
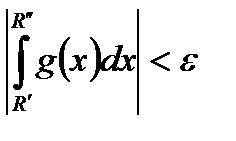Враховуючи умову 1) теореми, маємо, що функція 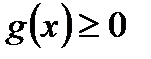для , а це означає, що і 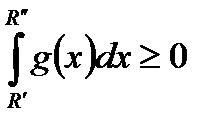, тобто модуль в останній нерівності можна зняти.

За властивостями інтеграла Римана маємо:

.

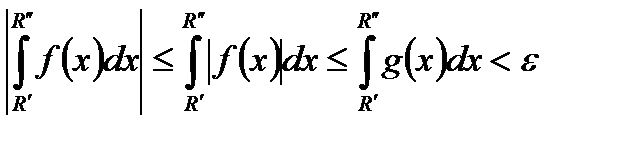Таким чином, для 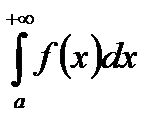маємо виконання критерію Коші збіжності.

Приклад. Розглянемо невласний інтеграл 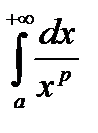, де 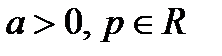. Зясуємо, при яких значеннях параметру 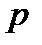цей інтеграл є збіжним. Нехай спочатку 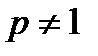. В цьому випадку:

.

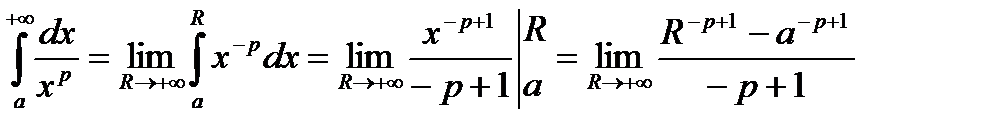Отримана границя існує, а поданий інтеграл збігається, якщо 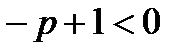, тобто 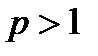. Якщо 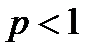, то інтеграл розбігається.

Залишилося розглянути випадок, коли :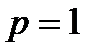

.

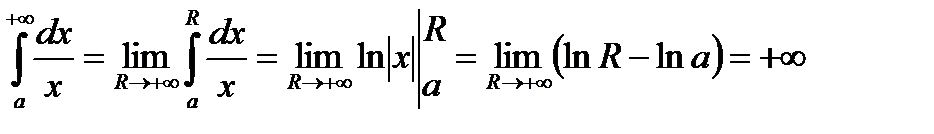Таким чином,

Питання

1. Визначення невласного інтегралу І роду.

2. Умова Коші в точці для функції однієї змінної.

3. Критерій існування границі функції однієї змінної.

4. Коли невласний інтеграл І роду називається збіжним (розбіжним)? Навести приклади збіжних (розбіжних) невласних інтегралів.

5. Критерій Коші збіжності НІ І роду.

6. Як повязана збіжність (розбіжність) інтегралів ?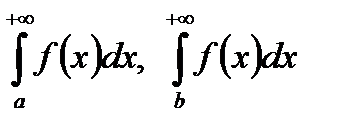

7. Загальна достатня умова збіжності невласного інтегралу І роду.