Визначення поверхневого інтегралу І типу
Нехай 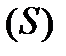 - двобічна гладка чи кусково-гладка поверхня. На
- двобічна гладка чи кусково-гладка поверхня. На 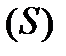 визначена функція
визначена функція 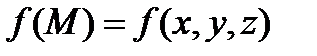 . Розібємо
. Розібємо 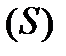 за допомогою довільних кусково-гладких кривих на частки
за допомогою довільних кусково-гладких кривих на частки 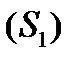 ,
, 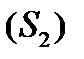 , ...,
, ..., 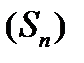 . Візьмемо довільно в кожній частці
. Візьмемо довільно в кожній частці 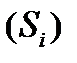 точку
точку 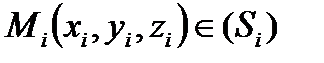 і обчислимо
і обчислимо 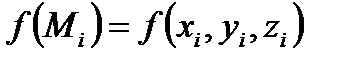 . Значення
. Значення  помножимо на площу
помножимо на площу 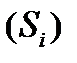 , яку позначатимемо
, яку позначатимемо 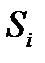 , тоді сума
, тоді сума
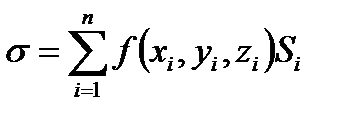
Називається інтегральною сумою для поверхневого інтеграла І типу.
Позначимо:
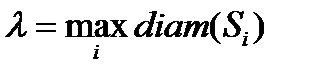 .
.
Визначення. Якщо існує
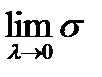 ,
,
яка не залежить ні від способу розбивки 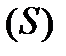 на частки, ні від вибору проміжкових точок
на частки, ні від вибору проміжкових точок 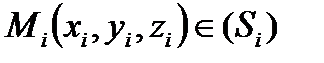 , то ця границя називається поверхневим інтегралом І типу від функції
, то ця границя називається поверхневим інтегралом І типу від функції 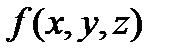 по поверхні
по поверхні 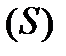 і позначається
і позначається
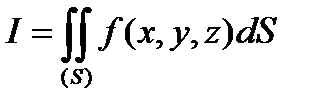 .
.
Дата добавления: 2015-08-21; просмотров: 736;
