Двобічні і однобічні поверхні

Лекція 46. Поверхневі інтеграли І типу

План

1. Двобічні і однобічні поверхні
2. Визначення поверхневого інтегралу І типу
3. Обчислення поверхневого інтегралу І типу

Двобічні і однобічні поверхні

Нехай поверхня визначена явно за допомогою рівняння

.

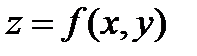Така поверхня не обмежує ніяке тіло, вона є незамкненою. Тут можна визначити верхню і нижню сторони поверхні. Якщо поверхня обмежує якесь тіло, то для неї можна визначити внутрішню і зовнішню сторони.

Розглянемо гладку поверхню 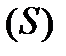, яка може бути замкненою чи обмеженою кусково-гладким контуром. В кожній точці такої поверхні до неї можна провести дотичну площину. Візьмемо на поверхні деяку точку 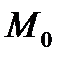, побудуємо в ній нормаль визначеного напрямку. Побудуємо на поверхні замкнений контур 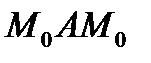, який не перетинає меж поверхні. Будемо обходити цей контур, будуючи в кожній його точці нормаль до поверхні (неперевно змінюючи нормаль). При поверненні в точку 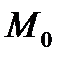можливі два випадки:

· Ми повернемося в 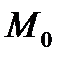з тим же нарямком нормалі, з яким виходили з неї;

· Ми повернемося в 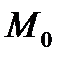з протилежним нарямком нормалі.

Якщо для поверхні завжди має місце перший випадок, то поверхня є двобічною, якщо для поверхні можливим є другий випадок, то поверхня однобічна. Прикладом однобічної поверхні є лист Мьобіуса.

Далі розглядаємо лише двобічні поверхні.

Визначення. Сукупність усіх точок поверхні з визначеними напрямками нормалей в них називається стороною поверхні.

Приклад. Нехай поверхня визначена за допомогою рівняння 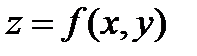, функція 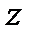неперервна в деякій област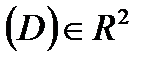і , і 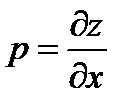, 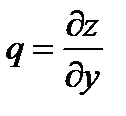- неперервні в 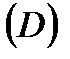.Тоді направляючі косінуси нормалі до поверхні мають вид:

, , .

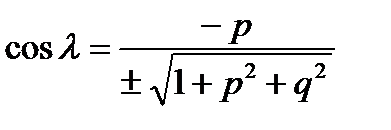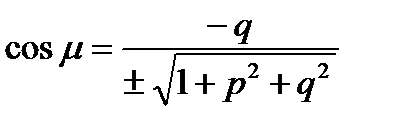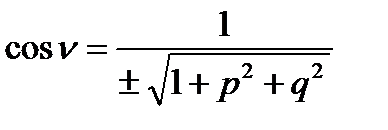Якщо 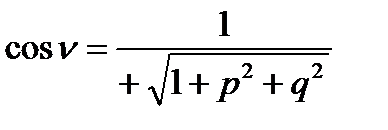, то кут між поверхнею і віссю OZменше за 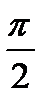, визначена верхня сторона поверхні, для 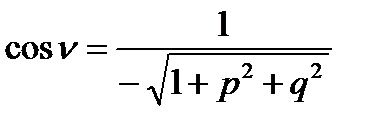визначається нижня сторона поверхні.