Обчислення обєму тіла за допомогою поверхневого інтегралу
Нехай тіло 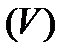 обмежено гладкими поверхнями:
обмежено гладкими поверхнями:
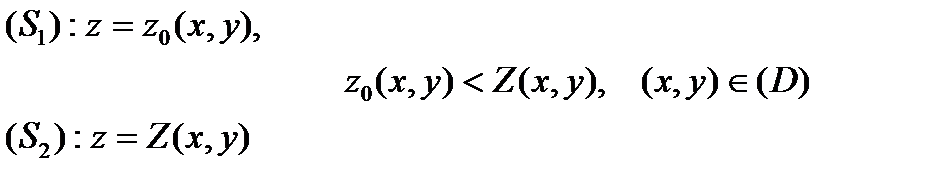
і циліндричною поверхнею 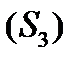 , твірна якої паралельна осі OZ(рис.3).
, твірна якої паралельна осі OZ(рис.3).
З геометричного змісту подвійного інтегралу витікає, що
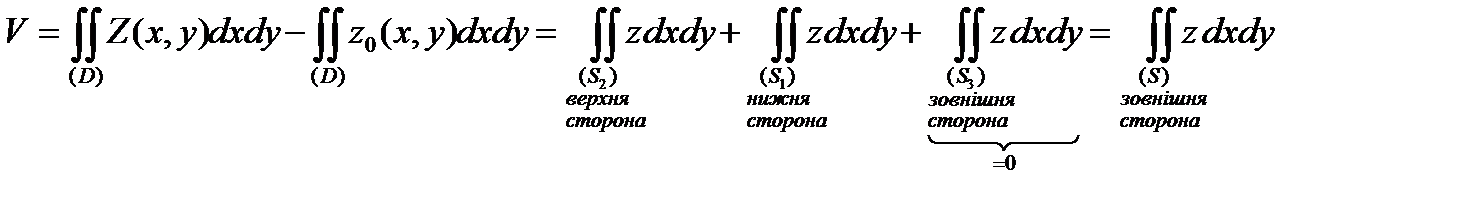 ,
,
де 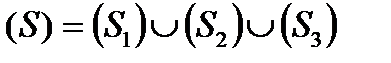 .
.
Отримана формула для обчислення обєма має місце для тіл, які можливо розбити на частки виду, представленого на рис.3 (циліндричні тіла І типу), за допомогою циліндричних поверхонь з твірною, паралельною осі OZ.

Рис.3.
Для циліндричніх тіл ІІ типу (ІІІ типу) з твірною, паралельною осі OХ (ОУ) мають місце формули для обчислення обєму:
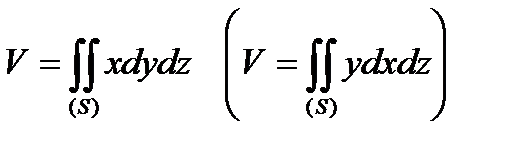 .
.
Якщо тіло є одночасно циліндричним тілом І, ІІ і ІІІ типу, то для обчислення його обєму мають місце всі три формули. Якщо ці формули скласти почленно, отримаємо загальну формулу для обчислення обєму:
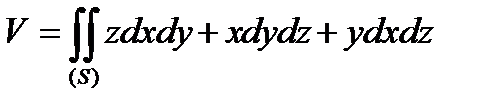 ,
,
де інтеграл береться по зовнішній стороні поверхні 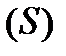 .
.
Дата добавления: 2015-08-21; просмотров: 831;
