Вибір нафтогазоперспективних об’єктів до першочергового пошукового буріння за допомогою експертних систем
Підвищення геологічної результативності та економічної ефективності пошуково-розвідувальних робіт на нафту і газ значною мірою залежить від достовірності і точності оцінки перспектив нафтогазоносності окремих локальних об’єктів. Донедавна, за умов адміністративного регулювання та значного бюджетного фінансування нафтогазової галузі, недостатня достовірність і точність прогнозу нафтогазоносності конкретних локальних структур компенсувалися здебільшого збільшенням обсягів пошуково-розвідувального буріння. В умовах ринкової економіки таке вирішення проблеми є неприпустимим. Постало нагальне завдання радикального підвищення достовірності і точності прогнозу можливої продуктивності нафтогазоперспективних структур в конкретних геологічних умовах. Вирішення цієї проблеми потребує використання науково обгрунтованої методики локального прогнозування з залученням новітніх прогресивних технологій його проведення. Перспективним напрямом розв’язання цього завдання є розроблення та впровадження комп’ютеризованих експертних систем для прогнозу нафтогазоносності локальних структур. Застосування таких експертних систем допомагає побудувати геологічні моделі об’єктів досліджень з метою відтворення окремих елементів геологічної історії та створити комп’ютерну технологію комплексної інтерпретації всієї наявної сукупності геолого-геофізичних і геохімічних показників при вирішенні конкретних геологічних завдань.
При якісній оцінці перспектив нафтогазоносності проблемним моментом є вибір нафтогазоперспективних об’єктів (локальних структур) для першочергової постановки пошукового буріння. Для вирішення цієї проблеми в практику пошукових робіт доцільно залучати методи розпізнавання образів, які базуються на принципі аналогій і використанні надійних статистичних методів обробки. В процесі розпізнавання образів проводяться науково-прикладні дослідження за допомогою обчислювальних процедур, які дають змогу сформулювати правила для встановлення належності деякого об’єкта до одного із заздалегідь виділеного класу об’єктів (образу).
Загальною умовою при цьому є вимога, щоби на досліджуваній території вже було певне число розвіданих “порожніх” структур і структур із встановленою продуктивністю, за матеріалами яких знаходяться статистичні критерії продуктивності або непродуктивності структур даного нафтогазоносного регіону.
Основою для знаходження критеріїв продуктивності або непродуктивності структур виступають геолого-геофізичні дані по групі розбурених “порожніх” і продуктивних структур. Мінімально необхідне число таких розбурених структур залежить від складності району досліджень і коливається в межах 10–20.
Кількість вихідних геолого-геофізичних показників в різних варіантах (методиках) прогнозу змінюється від 18–20 до 40. Проте досвід досліджень показав, що без особливих втрат для ефективності число показників може бути скорочене до 10–15 характеристик, що описують літолого-фаціальні особливості прогнозованого комплексу відкладів, структурні особливості пасток, геохімічні і гідродинамічні особливості даної ділянки території досліджень. Достовірність прогнозу при цьому досягає 80–90 %. На думку О.І. Холіна, саме цей напрям в методиці прогнозу є найбільш перспективним. Ним же показано, що у всіх без винятку випадках “порожні” структури пізнаються важче, ніж продуктивні. Більшість помилок припадає на “порожні” структури. Завдяки цьому виникає можливість повного виключення помилок по продуктивних структурах при прийнятному числі помилкових і неоднозначних висновків на “порожніх” об’єктах.
При використанні математичних методів для прогнозу нафтогазоносності локальних структур першочергове значення має вибір геологічної моделі об’єктів прогнозу. Геологічна постановка завдання повинна містити виділення основних етапів формування і наступну еволюцію покладів нафти і газу, орієнтовну оцінку ролі кожного з етапів у конкретних умовах даної нафтогазоносної області і вже на цій основі визначення вихідної сукупності геолого-геофізичних показників, які повинні бути використані для визначення критеріїв можливої продуктивності локальних структур.
Пошук критеріїв поділу локальних структур на “порожні” і продуктивні здійснюється за двома відомими еталонними вибірками. Всі запропоновані методи представляють собою різноманітні модифікації задачі розпізнавання образів.
З геолого-математичних позицій запропоновані методи можна поділити на дві групи:
1) група методів, в яких використовуються чисто статистичні підходи;
2) група методів, в яких використовуються сполучення детермінованого і статистичного розгляду задачі.
При чисто статистичному підході користуються довільним набором роздільних характеристик об’єктів двох класів. Детермінований підхід полягає в тому, що при конструюванні вихідної геологічної моделі об’єктів, які належить розпізнати, прагнуть до організації системи вихідних показників на основі детермінованої схеми утворення і еволюції покладів нафти і газу. Систему показників можна будувати із характеристик, які відображають фактори, що зумовлюють виникнення покладів, або орієнтуватися на показники, пов’язані з умовами збереження покладів, або, нарешті, шукати критерії розподілу структур на “порожні” і продуктивні, спираючись на характеристики, що зумовлені наявністю покладів нафти і газу.
Геологія – наука, що базується на спостереженнях, зокрема на тих, що містять значну частку невизначеності. Відкриття родовищ має ймовірнісний характер, тому логічним є застосування одного з методів теорії ймовірності – розпізнавання образів. Його суть полягає в порівнянні геологічних ознак досліджуваного об’єкта (локальної нафтогазоперспективної структури) з такими ж геологічними ознаками інших відомих об’єктів – еталонів (відкритих родовищ і “порожніх структур”), і в результаті робиться висновок про найбільш правдоподібну їхню відповідність. При цьому процес розпізнавання проводиться в три стадії (навчання, контроль методу, іспит). Комплекс геологічних ознак необхідно підбирати так, щоб вони мали якомога меншу мінливість (дисперсію) всередині класів, і якомога більшу різницю між класами.
Існує дві процедури розпізнавання образів при експертизі нафтогазоносності надр: паралельна і послідовна. При паралельній процедурі використовується відразу вся можлива інформація і проводиться одне підсумкове обчислення на її основі. Реалізація цієї процедури може бути здійснена такими способами, як дискримінантний аналіз, метод Кульбака та ін. Проте згадані традиційні процедури перевірки геолого-статистичних гіпотез при розпізнаванні перспективних локальних структур передбачають постійний для кожної конкретної задачі (розпізнаваної структури) набір критеріїв продуктивності. Так, у методі дискримінантного аналізу на основі значень m критеріїв продуктивності xіj (i=1..N, j=1..m) для деякої кількості N еталонних об’єктів, будується дискримінантна функція, що має вигляд:
| D(x) = a1xi1+a2xi2+…+amxim | (11.4 ) |
При розпізнаванні структур за допомогою такої функції необхідно визначити всі m ознак для кожної структури, що не завжди доцільно з економічної точки зору, адже не всі властивості однаково інформативні (важливі) для розпізнавання.
Таким чином, виникає потреба формулювання такої процедури розпізнавання, яка враховувала би неоднакову вагу (інформативність) властивостей об’єктів. Одна з процедур цього класу реалізована в інформаційному методі Кульбака. В цьому методі за сукупністю еталонних об’єктів на основі критерію відношень імовірностей будується процедура розпізнавання, яка використовує фіксовану кількість властивостей об’єктів. Вибір властивостей проводиться простим поділом за коефіцієнтом інформативності властивості: якщо величина коефіцієнта інформативності j-ої ознаки менша за певну наперед вибрану величину (поріг) h, то ця ознака не бере участі в розпізнаванні.
У випадку послідовної процедури здійснюється перехід від однієї змінної до іншої з врахуванням інформації, одержаної на кожному кроці, послідовно для всіх ознак. В підсумку послідовна процедура після того як зібрана вся інформація повинна дати той же самий результат, що й паралельна процедура. Якщо ж для одержання якогось висновку постійно необхідна вся інформація, то різниця між цими процедурами чисто символічна.
Отже, якщо якийсь висновок може бути одержаний на основі використання лише частини всієї можливої інформації, то більш доцільно застосовувати послідовну процедуру, оскільки результат вдається одержати набагато швидше.
Розглянемо реалізацію послідовного статистичного аналізу
А. Вальда з метою вибору першочергових об’єктів для пошукового буріння. Для певного нафтогазоносного регіону вибирається певна кількість еталонних об’єктів двох альтернативних класів з різко протилежними властивостями, а саме:
1) клас П – продуктивні структури, до яких відносяться структури з доказаною промисловою нафтогазоносністю, тобто відкриті родовища нафти і газу;
2) клас Н – непродуктивні (або “порожні”) структури, до яких належать структури, виведені з пошукового буріння як такі, на яких відсутня промислова нафтогазоносність, тобто структури з доведеною непродуктивністю.
Обидва класи структур мають бути охарактеризовані кількісними геологічними ознаками. До таких кількісних геологічних ознак можуть бути віднесені різноманітні риси і властивості нафтогазопошукових об’єктів, які мають кількісний вираз (наприклад, товщина нафтогазоносного комплексу, товщина регіональної породи-покришки, коефіцієнт інтенсивності структури, мінералізація пластових вод тощо). Числові значення цих геологічних ознак обидвох груп структур за допомогою спеціальної статистичної процедури Стерджеса розбиваються на діапазони. Для кожного діапазону значень геологічної ознаки вираховується відношення ймовірностей потрапляння об’єктів класу П і Н в цей діапазон. На основі цього відношення за спеціальною процедурою формуються коефіцієнти правдоподібності. Потім для кожної геологічної ознаки вираховуються коефіцієнти інформативності і формується послідовний спадний ряд за їхнім рангом.
Розподіл об’єктів на класи (продуктивні і непродуктивні об’єкти) проводиться шляхом накопичення коефіцієнтів правдоподібності окремих геологічних ознак в порядку спадання їхньої інформативності до тих пір, поки одержана сума не дозволить прийняти рішення про віднесення нерозпізнаного об’єкта до одного із альтернативних класів.
Оперуючи банком даних критеріїв нафтогазоносності структур певного регіону, можна підтвердити чи відкинути гіпотезу про перспективність локальної структури, а на основі одержаних результатів визначити об’єкти для постановки першочергового пошукового буріння. Проведені нами дослідження послідовного критерію відношення ймовірностей для підвищення ефективності розпізнавання локальних структур на нафтогазопродуктивність показали, що цей критерій вимагає, по крайній мірі, наполовину меншої кількості спостережень, ніж критерій, заснований на фіксованій кількості спостережень.
Будь-яке розпізнавання локальних геологічних структур неможливе без певного правила розпізнавання. Таке правило не може бути наперед заданим через різноманітність властивостей продуктивних і непродуктивних структур. Наприклад, і продуктивні, і непродуктивні структури можуть мати однакову пористість та проникність пластів, внаслідок чого відрізнити їх за цими властивостями неможливо. Тому в регіоні досліджень необхідно вибирати групи локальних структур з уже встановленою продуктивністю (клас П) та з уже встановленою непродуктивністю (клас Н). Такі структури є еталонними. Для цих структур визначимо весь комплекс критеріїв продуктивності, тобто властивостей, за якими їх можна віднести до одного з класів.
Наступним кроком досліджень є формування дерева рішень, тобто такої функції від набору критеріїв продуктивності, яка би давала одне значення для еталонних об’єктів класу Н та інше – для еталонних об’єктів класу П. Як показують наведені вище теоретичні положення, таке дерево може бути побудоване шляхом порівняння умовних розподілів імовірностей геологічних ознак на двох класах еталонних об’єктів.
Побудова умовних рядів розподілу вибраних нами критерійних ознак грунтується на вибірковому методі досліджень.
Оскільки істинні закони розподілу ознак невідомі, замість самого розподілу ймовірностей f(x) ми використовуємо умовний розподіл частостей (емпіричних імовірностей) p(x). Для цього діапазон зміни кожної j-ої ознаки ділиться на інтервали. Довжина інтервалу для j-ої ознаки hj визначається за формулою Стерджеса:
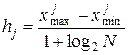 , ,
| (11.5) |
де 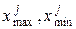 – відповідно найбільше та найменше значення j-ої ознаки в обох класах структур;
– відповідно найбільше та найменше значення j-ої ознаки в обох класах структур;
N – сумарна кількість структур в обох класах.
Після цього слід для кожної j-ої ознаки визначити кількість структур класу П і класу Н, значення ознаки в яких лежать в межах цих інтервалів.
Наступним кроком має стати визначення умовних рядів розподілу частостей кожної j-ої ознаки. Для цього застосуємо формули:
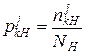 , , 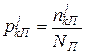 , ,
| (11.6) |
де 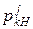 ,
,  – умовні частості j-ої ознаки в k-му інтервалі відповідно для класів непродуктивних та продуктивних структур;
– умовні частості j-ої ознаки в k-му інтервалі відповідно для класів непродуктивних та продуктивних структур;
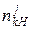 ,
,  - умовні частоти j-ої ознаки в k-му інтервалі відповідно для класів непродуктивних та продуктивних структур;
- умовні частоти j-ої ознаки в k-му інтервалі відповідно для класів непродуктивних та продуктивних структур;
NН, NП – кількості відповідно непродуктивних та продуктивних структур.
На основі визначених умовних рядів розподілу частостей треба обчислити критерій відношення ймовірностей для k-го інтервалу j-ої ознаки, який для зручності подальшого використання подамо в логарифмічній формі:
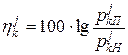 . .
| (11.7) |
Логарифмічна форма відношення ймовірностей називається коефіцієнтом правдоподібності k-го інтервалу j-ої ознаки.
За міру важливості j-ої ознаки для експертизи було взято коефіцієнт інформативності
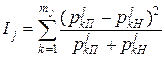 , ,
| (11.8) |
де mj – кількість інтервалів для j-ої ознаки.
Характерні ознаки повинні бути розташовані в порядку зменшення коефіцієнта інформативності, так щоб для експертизи можна було спочатку брати найінформативніші ознаки.
Для формулювання вирішувального правила спочатку слід задати значення ймовірностей похибок першого роду a та другого роду b (звичайно беруть a = b). Після цього необхідно знайти критичні значення T1 та T2 коефіцієнта правдоподібності (пороги класів Н і П) за формулами:
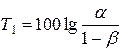 , , 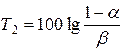 . .
| (11.9) |
Дерево рішень для віднесення об’єкта, що підлягає експертизі, до одного з двох альтернативних класів будується в такій послідовності:
1) додаються коефіцієнти правдоподібності перших двох ознак (за спадним рядом інформативності) для даного об’єкта;
2) якщо сума перевищує T2, то робиться висновок, що об’єкт належить до класу П. Якщо сума менша за T1, то робиться висновок, що об’єкт належить до класу Н;
3) якщо сума знаходиться в межах між T1 та T2 , то береться значення коефіцієнта правдоподібності наступної у спадному ряді інформативностей ознаки, і додається до суми перших, після чого переходять до пункту 2.
Додавання повторюється доти, доки не буде зроблено певний висновок або доки ще є ознаки. Якщо простір ознак вичерпано, а об’єкт так і не віднесений до певного класу, то об’єкт вважається нерозпізнаним, тобто таким, що потребує додаткових геологічних досліджень.
Якість сформованого дерева рішень оцінюється перевіркою (іспитом) на еталонних структурах. При цьому можливі три випадки:
1) еталонна структура визначена правильно;
2) еталонна структура одного класу визначена як структура іншого класу, тобто неправильно;
3) еталонна структура даним методом не визначається, тобто наявних геологічних ознак недостатньо для прийняття рішення щодо її належності до одного з альтернативних класів структур.
Останні два випадки, безумовно, слід трактувати як помилки у побудові геологічної моделі. Тому такі випадки слід брати на облік і в разі високої частки помилок (більш як 30 % від загальної кількості еталонних структур) будувати інший комплекс критерійних ознак або поповнювати банк еталонних структур з метою зменшення частки неправильно визначених під час іспиту еталонних локальних структур.
Крім послідовного методу, заснованому на ідеї А. Вальда, існують паралельні методи прогнозування, основним з яких є дискримінантний аналіз.
Дискримінантний аналіз є статистичним методом розпізнавання образів, що дозволяє вивчати розбіжності між двома і більше групами об’єктів (образами) за декількома змінними одночасно і на основі цих розбіжностей відносити певний об’єкт до тієї чи іншої групи (образу). Цей метод надзвичайно корисний для прогнозування у природничих та технічних науках, зокрема в нафтогазовій геології. Метод дискримінантного аналізу широко використовується як методологічна основа для комп’ютеризованого експертного прогнозування нафтогазоносності надр. Розглянемо формальну постановку задачі прогнозування нафтогазоносності надр, яка приводить до необхідності застосування даного методу.
У деякому нафтогазоносному регіоні поряд з відкритими родовищами вуглеводнів є площі, на яких необхідно визначити доцільність пошукового буріння на нафту і газ ще до його початку. В межах цих площ геофізичними методами, структурним бурінням, а також геохімічними методами виділено ряд локальних структур, в яких виявлено сприятливі умови для скупчень в них вуглеводнів. Вивчаючи параметри вже відомих нафтових та газових покладів (клас П – продуктивні) та структурних об’єктів, що за результатами попереднього пошукового буріння не дали припливу нафти і газу (клас Н – непродуктивні), експертна система повинна знайти відповідь на такі питання:
– які з цих параметрів можуть бути корисними для передбачення покладів у підготовлених локальних об’єктах;
– як ці параметри можуть бути зв’язані в математичну функцію для передбачення найбільш імовірного результату;
– яка точність прогнозування.
Дискримінантний аналіз може забезпечити одержання необхідних даних для вирішення цих питань. Якщо деякі змінні, взяті для відкритих покладів (об’єктів класу П), відрізняються від відповідних змінних для випадків, коли було встановлено непродуктивність підготовлених структур (об’єктів класу Н), то експертиза, що ґрунтується на дискримінантному аналізі, може допомогти прийняти рішення про проведення пошукового буріння на підготовлених локальних об’єктах у ситуації невизначеності.
Основним припущенням дискримінантного аналізу є те, що існують дві чи більше групи геологічних об’єктів, що за деякими змінними відрізняються одна від одної, причому такі змінні можуть бути виміряні за інтервальною шкалою або за шкалою відношень. Дискримінантний аналіз допомагає виявляти розбіжності між групами і дає можливість чітко класифікувати об’єкти за принципом максимальної подібності.
Об’єкти (спостереження) повинні належати до одного з двох (чи більше) класів (груп). Об’єкти є основними одиницями аналізу. У нашій задачі прогнозування нафтогазоносності кожна локальна структура є об’єктом. Клас повинен бути визначений таким чином, щоб кожне спостереження належало до одного і тільки одного класу. Кожна локальна структура може бути віднесена до одного з двох класів: випадки успішного пошукового буріння з отриманням промислового припливу нафти і газу і випадки, коли такого припливу не отримали.
Дискримінантний аналіз – це загальний термін, що відноситься до декількох тісно пов’язаних статистичних процедур. У конкретних ситуаціях не обов’язково використовувати всі ці процедури. Їх можна розділити на методи інтерпретації міжгрупових розбіжностей і методи класифікації спостережень за групами. Мова йде про інтерпретацію, коли розглядаються розбіжності між класами. Іншими словами, при інтерпретації необхідно відповісти на питання: чи можливо, використовуючи даний набір характеристик (змінних), чітко відрізнити один клас від іншого; наскільки добре ці характеристики дозволяють провести розпізнавання і які з них найбільш інформативні. Метод, що відноситься до класифікації, пов’язаний з одержанням однієї чи декількох функцій, що забезпечують можливість віднести даний об’єкт до однієї з груп. Ці функції, що називаються дискримінантними, залежать від значень характеристик таким чином, що з’являється можливість віднести кожен об’єкт до однієї з груп. Наприклад, якщо значення характеристик нового об’єкта близькі до відповідних значень для об’єкта – представника класу П (відкритих покладів), дискримінантна функція покаже, що для розглянутого об’єкта більш імовірний позитивний результат. (Після того як буде пробурено пошукову свердловину, стане відомо, чи виправдався прогноз, однак іноді підтвердити точність класифікації неможливо). Зрозуміло, що дискримінантний аналіз необхідний і для інтерпретації, і для класифікації.
Характеристики, що застосовуються для того, щоб чітко відрізняти один клас від іншого, називаються дискримінантними змінними або геологічними критерійними ознаками. Ці змінні повинні вимірюватися або за інтервальною шкалою, або за шкалою відношень. Тоді стає можливим обчислення математичних сподівань, дисперсій і правомірне використання дискримінантних змінних у геолого-математичних рівняннях. У загальному випадку число дискримінантних змінних необмежене, але в сумі число об’єктів обох класів завжди повинне перевищувати число змінних принаймні на два.
Проте, існують певні обмеження, що стосуються статистичних властивостей дискримінантних змінних. По-перше, жодна змінна не може бути лінійною комбінацією інших змінних. Лінійна комбінація – це сума двох чи більше змінних з постійними коефіцієнтами. Таким чином, не можна скористатися сумою змінних чи їх середнім арифметичним разом із самими змінними. Відповідно неприпустимі змінні, лінійно залежні між собою, для яких коефіцієнт кореляції дорівнює 1. Змінна, що є лінійною комбінацією інших, не несе якої-небудь нової інформації, крім тієї, яка міститься в компонентах суми, тому вона є зайвою. Наприклад, до складу критерійних ознак не можуть входити одночасно нафтонасиченість порід та водонасиченість, оскільки їхня сума дорівнює одиниці.
Наступне припущення стосується того, що закон розподілу для кожного класу є багатовимірним нормальним, тобто кожна змінна має нормальний розподіл при фіксованих інших змінних. Дане припущення дозволяє одержати точні значення ймовірності належності до даного класу і критерію значущості. При порушенні припущення про нормальність розподілу значення ймовірності обчислити точно вже не можна, але відповідні оцінки можуть бути корисні, якщо, звичайно, дотримуватися відомої обережності.
Згадані вище припущення для дискримінантного аналізу фундаментальні. Якщо експериментальні дані для деякої конкретної задачі не цілком задовольняють ці припущення, то статистичні висновки не будуть точним відображенням дійсності.
Дата добавления: 2015-07-24; просмотров: 1271;
