Властивості інтегрованих функцій і подвійних інтегралів

1. Якщо змінити значення інтегрованої на 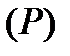функції 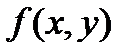вздовж будь-якої кривої 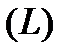з площею 0, то нова функція також буде інтегрованою на 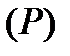, а її інтеграл буде співпадати з інтегралом від .

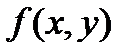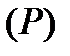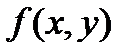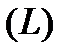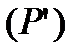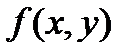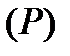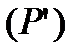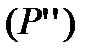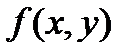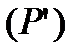2. Якщо область , на якій визначена , кривою з площею 0 розкладена на і , то з інтегрованості функції на витікає її інтегрованість на і , і навпаки: з інтегрованості на і 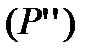витікає інтегрованість 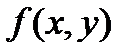на 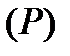. При цьому:

.

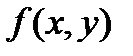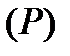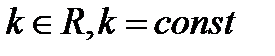3. Якщо функція інтегрована на , а , то

.

Завдання. Записати інші властивості подвійних інтегралів (Фихтенгольц, т.ІІІ, с.127-134).