Визначення ряду Фур’є по ортогональній системі функцій
Нехай 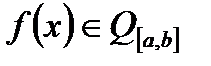 і
і
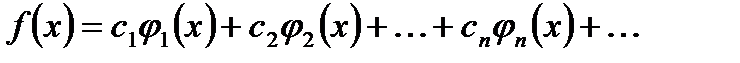 , (5)
, (5)
де 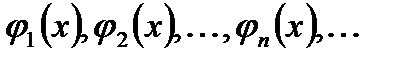 - ортогональна система функцій на
- ортогональна система функцій на 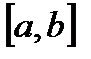 . Припустимо, що рівність (5) можливо почленно інтегрувати (це можливо, наприклад, тоді, коли ряд в правій частині рівності (5) збігається рівномірно). Домножимо (5) на
. Припустимо, що рівність (5) можливо почленно інтегрувати (це можливо, наприклад, тоді, коли ряд в правій частині рівності (5) збігається рівномірно). Домножимо (5) на 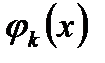 і проінтегруємо:
і проінтегруємо:
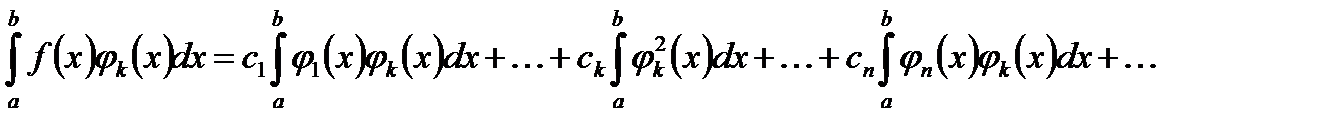 (6)
(6)
Всі інтеграли в правій частині останньої рівності дорівнюють 0, крім 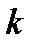 -го, завдяки ортогональності системи функцій
-го, завдяки ортогональності системи функцій 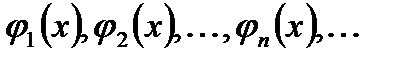 . Тоді (6) можна записати в вигляді:
. Тоді (6) можна записати в вигляді:

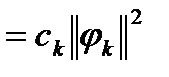 ,
,
звідки
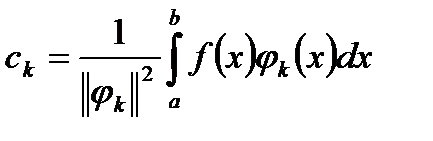 (7)
(7)
Щоб визначити 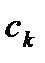 по формулі (7) немає необхідності вимагати почленного інтегрування ряду (5), достатньо, щоб
по формулі (7) немає необхідності вимагати почленного інтегрування ряду (5), достатньо, щоб 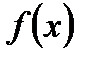 і
і 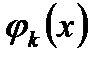 були інтегрованими, а це дійсно так, бо
були інтегрованими, а це дійсно так, бо 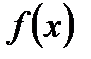 і
і 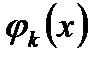
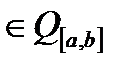 .
.
Тому 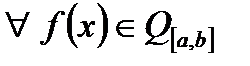 можна поставити в співвідношення ряд
можна поставити в співвідношення ряд
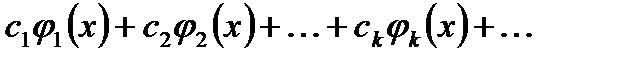 (8)
(8)
де 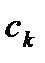 визначаються по формулі (7).
визначаються по формулі (7).
Ряд (8) називається рядом Фурьє для 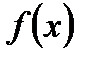 по ортогональній системі
по ортогональній системі 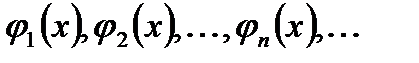
Запишемо ряд Фурьє для 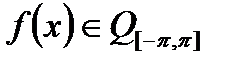 по ортогональній системі функцій
по ортогональній системі функцій 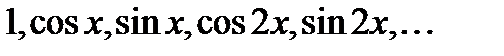
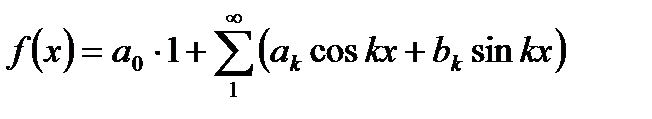 ,
,
де
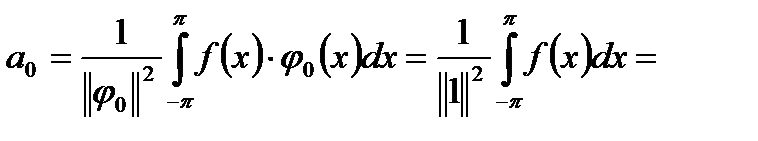
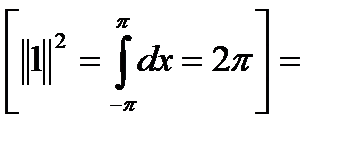
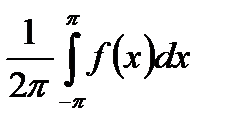 ;
;
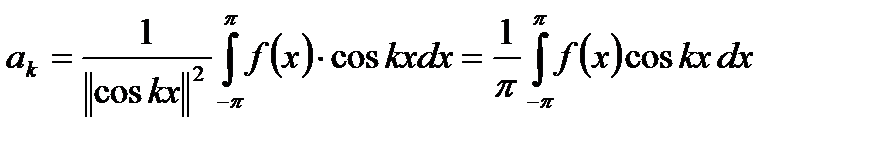 ;
;
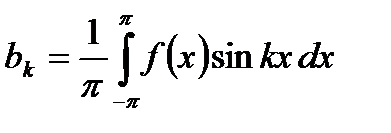 ,
, 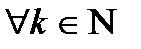 .
.
Питання
1. Яка функція 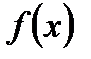 називається кусково-неперервною на
називається кусково-неперервною на 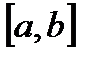 ? Навести приклади таких функцій?
? Навести приклади таких функцій?
2. Як значення інтегралу Римана від функції 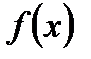 залежить від значення цієї функції в скінченній кількості точок?
залежить від значення цієї функції в скінченній кількості точок?
3. Які функції 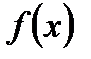 і
і 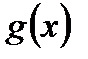 називаються еквівалентними на
називаються еквівалентними на 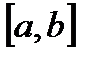 ? Навести приклади еквівалентних функцій.
? Навести приклади еквівалентних функцій.
4. Властивості відношення «~» для кусково-неперервних функцій.
5. Яка система функцій 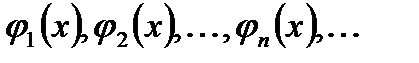 з
з 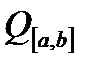 називається ортогональною?
називається ортогональною?
6. Що називається нормою 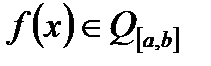 ?
?
7. Яка ортогональна система функцій 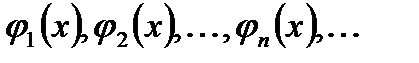 з
з 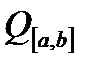 називається ортонормальною?
називається ортонормальною?
8. Як ортогональну систему можливо зробити ортонормальною?
9. Які системи функцій називаються основними тригонометричними системами?
10. Що називається рядом Фурьє для 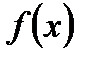 по ортогональній системі
по ортогональній системі 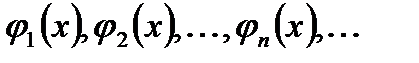 ?
?
Дата добавления: 2015-08-21; просмотров: 877;
