Еквівалентні функції
Лекція 50. Ряд Фур’є по ортогональній системі функцій
План
- Еквівалентні функції
- Визначення системи ортогональних функцій. Система ортонормованих функцій
- Тригонометричні системи ортогональних функцій
- Визначення ряду Фур’є по ортогональній системі функцій
Еквівалентні функції
Основою теми «Ряд Фур’є по ортогональній системі функцій» – це визначений інтеграл Римана. Відомо, що значення інтегралу 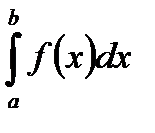 не зміниться, якщо значення підінтегральної функції змінити в скінченній кількості точок.
не зміниться, якщо значення підінтегральної функції змінити в скінченній кількості точок.
Визначення 1. Будемо називати функцію 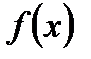 кусково-неперервною на
кусково-неперервною на 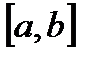 , якщо вона має на цьому сегменті
, якщо вона має на цьому сегменті 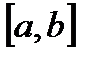 скінчену кількість точок розриву, є інтегрованою на
скінчену кількість точок розриву, є інтегрованою на 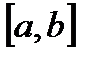 (можливо, навіть, у сенсі невласного інтегралу).
(можливо, навіть, у сенсі невласного інтегралу).
Визначення 2. Дві кусково-неперервні функції 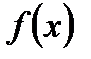 і
і 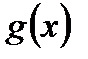 будемо називати еквівалентними на
будемо називати еквівалентними на 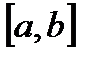 і позначати
і позначати 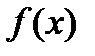 ~
~ 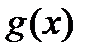 , якщо їх значення різні лише в скінченній кількості точок з
, якщо їх значення різні лише в скінченній кількості точок з 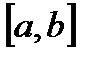 .
.
Для еквівалентних функцій 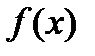 ~
~ 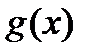 мають місце наступні властивості:
мають місце наступні властивості:
1) 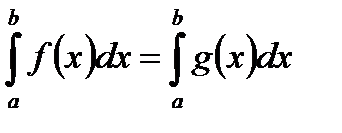 ;
;
2) для будь-якої функції 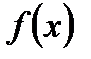 ~
~ 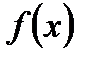 ;
;
3) якщо 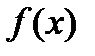 ~
~ 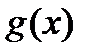 , то
, то 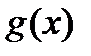 ~
~ 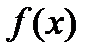 ;
;
4) якщо 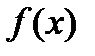 ~
~ 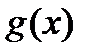 , і
, і 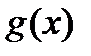 ~
~ 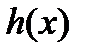 , то
, то  ~
~ 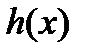 .
.
Таким чином, відношення «~» є відношенням еквівалентності на множині кусково – неперервних функцій, а це приводе до того, що множина кусково – неперервних функцій розпадається на класи еквівалентності. Між цими класами можливо ввести лінійні операції:
1) Складання двох класів (складання двох представників з классів);
2) Множення класу на дійсне число.
Таким чином, множину класів еквівалентних функцій ми перетворили в лінійний простір. Будемо позначати цей простір 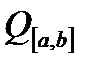 .
.
Дата добавления: 2015-08-21; просмотров: 1139;
