Умова існування подвійного інтегралу
Лекція 45. Властивості подвійного інтегралу
План
- Умова існування подвійного інтегралу
- Класи інтегрованих функцій
- Властивості інтегрованих функцій і подвійних інтегралів
- Формула Гріна
Умова існування подвійного інтегралу
Нехай в області 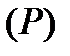 визначена функція
визначена функція 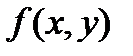 .
.
Теорема 1 (необхідна умова існування подвійного інтеграла). Якщо функція 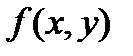 інтегрована на
інтегрована на 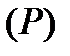 , вона обмежена на
, вона обмежена на 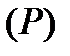 .
.
Нехай 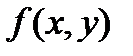 обмежена на
обмежена на 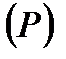 . Розібємо область
. Розібємо область 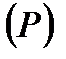 кривими на скінченну кількість часток
кривими на скінченну кількість часток 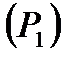 ,
, 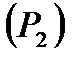 ,...,
,..., 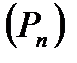 , площі яких відповідно дорівнюють
, площі яких відповідно дорівнюють 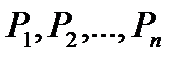 . Позначимо:
. Позначимо:
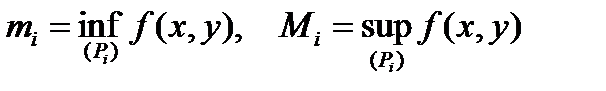 .
.
Визначення 1. Нижньою (верхньою) сумою Дарбу від функції 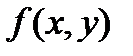 на області
на області 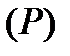 , що відповідає побудованій розбивці області
, що відповідає побудованій розбивці області 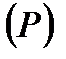 на частки
на частки 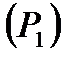 ,
, 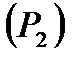 ,...,
,..., 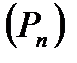 , називається
, називається
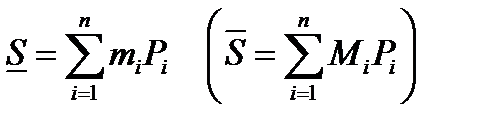 .
.
Властивості сум Дарбу для функції двох змінних 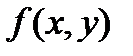 аналогічні властивостям сум Дарбу для функції одної змінної. Аналогічно визначаються нижній і верхній інтеграли Дарбу.
аналогічні властивостям сум Дарбу для функції одної змінної. Аналогічно визначаються нижній і верхній інтеграли Дарбу.
Теорема 2 (критерій існування подвійного інтегралу). Для того, щоб функція 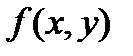 була інтегрована на
була інтегрована на 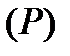 , необхідно і достатньо, щоб
, необхідно і достатньо, щоб
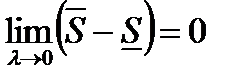 .
.
Дата добавления: 2015-08-21; просмотров: 1502;
