Вектор Умова

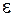Пусть в среде распространяется плоская монохроматическая волна (24.5). Выберем малый объем такой, чтобы скорость всех частиц и относительную деформацию можно было считать постоянными по всему объему. Скорость частиц найдем, дифференцируя смещение 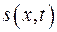по времени .

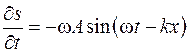Кинетическая энергия объема

.

Объем вследствие упругой деформации будет обладать также потенциальной энергией, причем для бегущей волны в каждый момент времени кинетическая и потенциальная энергии равны и изменяются в одинаковой фазе. Это является существенным отличием волнового процесса от колебаний в системе с сосредоточенными параметрами, где изменения кинетической и потенциальной энергий происходят в противофазе (см. § 4). С учетом этого для полной механической энергии объема можно записать

.

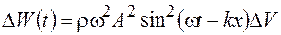Тогда объемная плотность энергии упругой волны

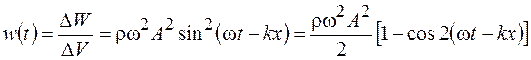. (27.1)

Из (27.1) видно, что объемная плотность энергии изменяется с удвоенной частотой и пропорциональна квадрату частоты и амплитуды волны. Усредняя (27.1) за период колебаний 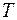, найдем среднее значение объемной плотности энергии:

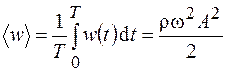. (27.2)

Возьмем произвольную поверхность 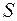. Количество энергии, переносимой волной через эту поверхность в единицу времени, называется потоком энергии :

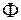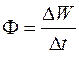. (27.3)

Как следует из определения, поток энергии измеряется в ваттах (Вт).

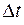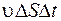Если поверхность перпендикулярна направлению распространения волны, а ее площадь мала, то за малое время через эту поверхность будет перенесена энергия , заключенная в объеме , где 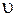– скорость волны. Так как объем мал, то, полагая, что объемная плотность энергии в этом объеме постоянная, получим 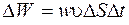. Разделив обе части последнего равенства на 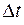, найдем поток энергии 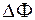через поверхность :

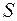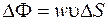. (27.4)

Отношение потока энергии, переносимого волной через поверхность 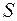, перпендикулярную направлению распространения волны, к площади этой поверхности называют плотностью потока энергии 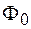, т. е. 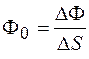. Плотность потока измеряется в 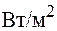. Введем вектор Умова ;

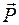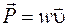. (27.5)

Вектором Умова называется вектор, направленный в сторону распространения волны (т. е. перпендикулярно волновой поверхности), величина которого равна произведению объемной плотности энергии и скорости распространения волны. Из (27.4) следует, что вектор Умова численно равен количеству энергии, переносимой волной в единицу времени через единицу площади поверхности, перпендикулярной направлению распространения волны. Единица измерения вектора Умова – 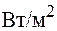. Зная вектор Умова 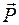, можно найти поток энергии через произвольную поверхность 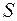по формуле

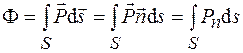, (27.6)

где 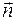– единичный вектор нормали к поверхности 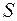; 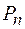– проекция вектора Умова на нормаль 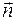к поверхности .

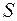Интенсивностью волны 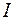называется среднее за период 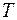значение потока энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны. Интенсивность волны равна среднему значению модуля вектора Умова и так же, как и вектор Умова, измеряется в 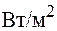, т. е.

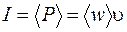. (27.7)

Подставляя вместо 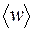выражение (27.2), получим

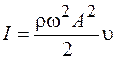. (27.8)

Из этого выражения следует, что интенсивность волны пропорциональна квадрату частоты и амплитуды.