Волновое уравнение. Поскольку волна представляет собой колебательный процесс, то подобно тому, как колебания в различных физических системах обладают целым рядом общих свойств

Поскольку волна представляет собой колебательный процесс, то подобно тому, как колебания в различных физических системах обладают целым рядом общих свойств, волны различной природы также обладают единством свойств и способов их описания. Одной из особенностей, отражающей это единство, является то, что волны, независимо от их физической природы, удовлетворяют одному и тому же дифференциальному уравнению, называемому волновым уравнением.

Рассмотрим плоскую монохроматическую волну, распространяющуюся в положительном направлении оси 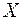. Найдем вторые частные производные по времени 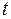и координате 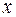от уравнения этой волны (24.5):

,

.

Разделив первое равенство на 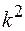, а второе на 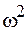, приравняем левые части полученных равенств:

.

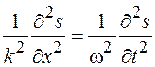С учетом (23.3) последнее уравнение можно записать в виде

. (25.1)

Полученное дифференциальное уравнение в частных производных второго порядка называется одномерным волновым уравнением, поскольку оно описывает волну, распространяющуюся вдоль оси 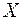. Если волна идет в произвольном направлении пространства, то в левой части уравнения (25.1) должна стоять сумма вторых частных производных по всем трем координатам, т. е. в общем случае волновое уравнение имеет вид

. (25.2)

Волновое уравнение получено для плоской волны, но оказывается, что независимо от формы волновой поверхности любая волна должна удовлетворять волновому уравнению (25.2) и, наоборот, если некоторая функция удовлетворяет волновому уравнению (25.2), то она описывает некоторую волну, распространяющуюся в пространстве. В каждом конкретном случае уравнение волны находится путем решения волнового уравнения (25.2) с учетом так называемых начальных и граничных условий. Следует обратить внимание также на то, что коэффициент при второй частной производной по времени равен величине, обратной квадрату скорости распространения волны.