Упругие волны в газах, жидкостях и твердых телах

Рассмотрим продольную волну, распространяющуюся в упругой среде вдоль оси 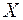. Смещение частиц среды относительно друг друга вдоль направления распространения волны приводит к возникновению периодических сжатий и разряжений в объеме среды.

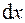Выберем элементарный объем среды в виде прямого цилиндра длиной и площадью основания 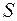(рис. 26.1). На цилиндр со стороны окружающей среды действуют упругие силы 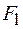и 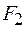, приложенные к основаниям цилиндра. По второму закону Ньютона для объема цилиндра можно записать

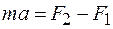, (26.1)

где 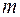– масса цилиндра; 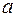– ускорение. Масса цилиндра равна произведению его объема на плотность среды 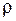, т. е. . Ускорение цилиндра равно второй производной по времени от смещения 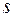, т. е. 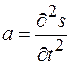. Силы 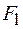и 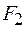выразим через напряжения в среде: 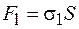и , где 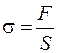– напряжение. Тогда уравнение (26.1) примет вид

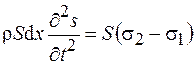. (26.2)

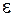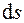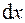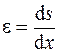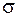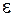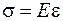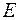Деформацию цилиндра будем характеризовать величиной относительной деформации , которая равна отношению удлинения цилиндра к его первоначальной длине , т. е. . По закону Гука в дифференциальной форме напряжение связано с относительной деформацией соотношением , где – модуль упругости Юнга. Подставив в уравнение (26.2) напряжения и сократив обе части на 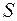, получим

. (26.3)

Выражение в скобках можно записать следующим образом:

,

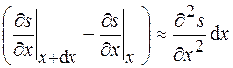и тогда (26.3) после сокращения на 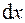примет вид

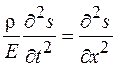. (26.4)

Уравнение (26.4) представляет собой одномерное волновое уравнение, и из него следует, что скорость распространения продольной упругой волны определяется упругими свойствами (модулем упругости Юнга 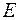) и плотностью среды, причем

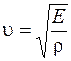. (26.5)

Как уже было отмечено выше, продольная упругая волна представляет собой чередование сжатий и разряжений среды. Упругими свойствами при сжатии и разряжении обладают как твердые тела, так и жидкости и газы, поэтому продольные упругие волны могут распространяться в любой среде.

В твердых телах кроме продольных могут распространяться поперечные волны. В поперечной волне смещение частиц происходит в направлении, перпендикулярном направлению распространения волны, т. е. происходит сдвиг смежных слоев среды относительно друг друга. При этом среда должна обладать достаточно высокой упругостью по отношению к деформации сдвига. Этим свойством обладают только твердые тела. В жидкостях и газах силы межмолекулярного взаимодействия гораздо слабее, чем в твердых телах и играют существенную роль только при уменьшении или увеличении расстояния между молекулами (т. е. при сжатии или разряжении среды). В отношении сдвига жидкости и газы практически не проявляют упругих свойств и поэтому поперечные волны в них распространяться не могут. Можно показать, что поперечные волны в твердых телах также удовлетворяют волновому уравнению, а скорость их распространения

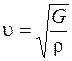, (26.6)

где 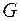– модуль сдвига; 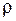– плотность среды.

При распространении упругой волны в газе действие упругой силы , возникающей при смещении молекул газа, приводит к изменению давления газа , поэтому в газовой среде по закону Гука

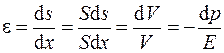, (26.7)

где знак "–" означает, что увеличение объема газа приводит к уменьшению его давления. Из (26.7) для модуля упругости газа получим

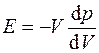. (26.8)

В большинстве случаев разрежения и сжатия газа чередуются так быстро, что выделенный элементарный объем газа не успевает обмениваться теплом с окружающей средой и процесс можно считать адиабатическим. Для адиабатического процесса давление и объем идеального газа связаны уравнением Пуассона

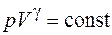, (26.9)

где 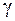– показатель адиабаты. Возьмем полный дифференциал от обеих частей уравнения (26.9):

.

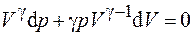Отсюда следует, что 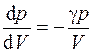и, подставляя это соотношение в (26.8) для модуля упругости газа, получим 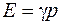. Из уравнения Менделеева–Клапейрона легко показать, что 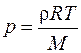, где 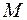– молярная масса газа; 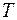– его температура; 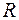– универсальная газовая постоянная, и тогда 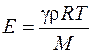. Подставляя полученное выражение модуля упругости в формулу (26.5), для скорости распространения упругих волн в газе будем иметь

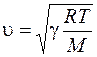. (26.10)

Таким образом, скорость упругих волн в газе зависит от температуры. Для воздуха ( 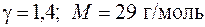) при имеем 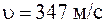, что хорошо согласуется с экспериментальными данными.