Монохроматическая бегущая волна

Пусть в некоторой точке О, где расположен источник волн, каким-либо образом возбуждается гармоническое колебание с амплитудой 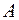и циклической частотой :

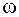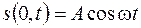. (23.1)

В точку Р, удаленную от источника на расстояние 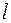вдоль направления распространения волны, колебания дойдут с некоторым запозданием 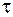, обусловленным конечной скоростью 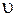распространения волны, причем 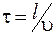. Тогда в этой точке колебания будут описываться выражением

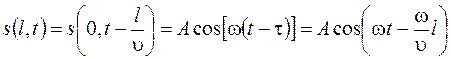. (23.2)

Отношение циклической частоты к скорости распространения монохроматической волны называется волновым числом

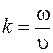. (23.3)

Тогда (23.2) можно записать в виде

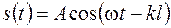. (23.4)

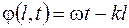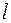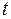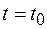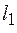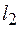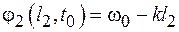Полученное выражение описывает монохроматическую волну, распространяющуюся в пространстве от источника, расположенного в начале координат. Величина называется фазой волны в точке, удаленной на расстояние от источника, в момент времени . Возьмем некоторый фиксированный момент времени и найдем фазу волны в двух точках, расположенных вдоль направления распространения волны на расстояниях и : ; . Выберем точки так, чтобы разность фаз 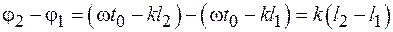равнялась . Это будет в том случае, если расстояние между точками равно 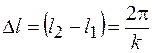. С учетом (23.3) это расстояние будет равно 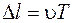, где – период колебаний. Произведение скорости распространения волны на период колебаний равно расстоянию, пройденному волной за время одного колебания, и называется длиной волны . Отсюда следует, что колебания в точках, удаленных друг от друга на расстояние, равное длине волны , в направлении распространения волны, происходят в одной фазе (или отличаются на ). Из вышеуказанного следует также, что волновое число связано с длиной волны соотношением

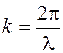. (23.5)

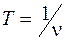Так как период колебаний связан с частотой соотношением , то легко убедиться, что

. (23.6)

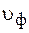Зафиксируем некоторое значение фазы волны и найдем скорость перемещения точки с фиксированной фазой колебаний. Для данной точки , откуда следует

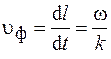. (23.7)

Скорость перемещения точки с фиксированной фазой колебаний называется фазовой скоростью.