Величина, равная разности оптических длин проходимых волнами путей, называется оптической разностью хода волн.
Из формулы (2.11.5) следует, что если оптическая разность хода равна целому числу длин волн в вакууме:
D = ± kl0 (k = 0,1,2,...), (2.11.7)
то разность фаз d = ± 2pk, и колебания, возбуждаемые волнами в точке P, будут происходить с одинаковой фазой. Следовательно, (2.11.7) - условие интерференционного максимума.
Если D равна полуцелому числу длин волн в вакууме:

 , (k = 0,1,2,...), (2.11.8)
, (k = 0,1,2,...), (2.11.8)
то d = ± (2pk + p), и колебания в точке совершаются в противофазе. Таким образом, (2.11.8) - условие интерференционных минимумов.
Рассчитаем интерференционную картину при наложении когерентных волн от двух действительных или мнимых источников S1 и S2, имеющих вид параллельных светящихся нитей или узких щелей (рис. 2.11.2).
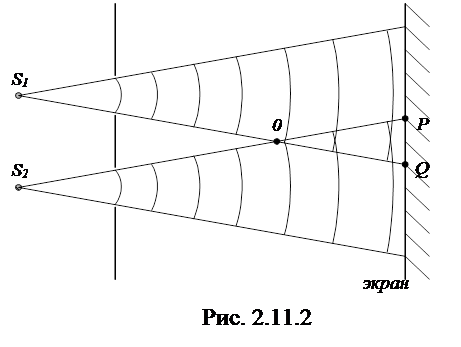 Область OPQ, в которой волны перекрываются называется полем интерференции. На экране будет видна интерференционная картина, которая в случае цилиндрических волнимеет вид чередующихся светлых и темных прямолинейных полос.
Область OPQ, в которой волны перекрываются называется полем интерференции. На экране будет видна интерференционная картина, которая в случае цилиндрических волнимеет вид чередующихся светлых и темных прямолинейных полос.
Определим ширину светлых и темных полос и их положения на экране. Для этого положение точки на экране будем характеризовать координатой x, отсчитываемой от точки 0, относительно которой S1 и S2 расположены симметрично (рис.2.11.3). Источники будем считать колеблющимися в одинаковой фазе.
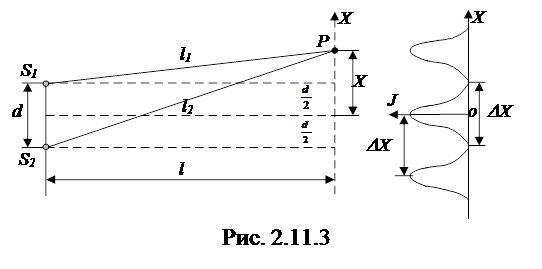 Из рис. 2.11.3 следует, что
Из рис. 2.11.3 следует, что
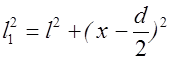
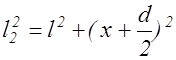 ,
,
откуда
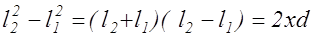 . (2.11.9)
. (2.11.9)
Как будет показано ниже, для получения различимой интерференционной картины необходимо, чтобы d<<l. Расстояние x также обычно значительно меньше l. При этих условиях в среде с n = 1 из (2.11.9) находим оптическую разность хода волн в точке экрана с координатой x:
 (2.11.10)
(2.11.10)
Из (2.11.10) и условия (2.11.7) находим координаты максимумов на экране
 (k = 0,1,2...). (2.11.11)
(k = 0,1,2...). (2.11.11)
Из (2.11.10) и условия (2.11.8) находим координаты минимумов
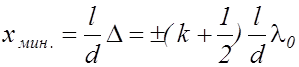 , (k = 0,1,2...). (2.11.12)
, (k = 0,1,2...). (2.11.12)
Найдем ширину светлойполосы с помощью (2.11.12). Очевидно, это расстояние между соседними минимумами,например, k-м и (k+1)-м равно
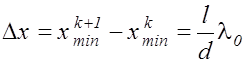 . (2.11.13)
. (2.11.13)
С помощью формулы (2.11.11) аналогично находим, что расстояние между соседними максимумами определяется таким же, как и (2.11.13) выражением:
 .
.
Как следует из выражения (2.11.13), отчетливая интерференционная картина будет наблюдаться при выполнении упоминавшегося выше условия:
d<<l.
Рассмотрим важный случай интерференции, который наблюдается при наложении встречных плоских гармонических волн с одинаковой частотой и амплитудой. Возникающий в результате колебательный процесс получил название стоячей волны. Стоячие волны возникают при наложении падающей на преграду волны и бегущей ей навстречу отраженной. Получим уравнение стоячей волны. Уравнения двух плоских волн, распространяющихся в противоположных направлениях, имеют вид:
x1=Acos(wt-kx),
x2=Acos(wt+kx).
Сложим уравнения волн и преобразуем результат по формуле суммы косинусов, тогда получим
x=x1+x2=2A coswt coskx.(2.11.14)
Учитывая, что волновое число 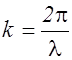 , уравнение (2.11.14) можно записать в виде
, уравнение (2.11.14) можно записать в виде
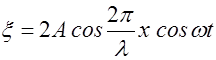 . (2.11.15)
. (2.11.15)
Уравнение (2.11.15) и есть искомое уравнение стоячей волны. Из уравнения стоячей волны следует, что в каждой точке среды происходят колебания той же частоты, что и у встречных волн, причем амплитуда колебаний зависит от x. В точках, координаты которых удовлетворяют условию
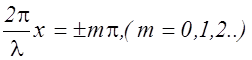 , (2.11.16)
, (2.11.16)
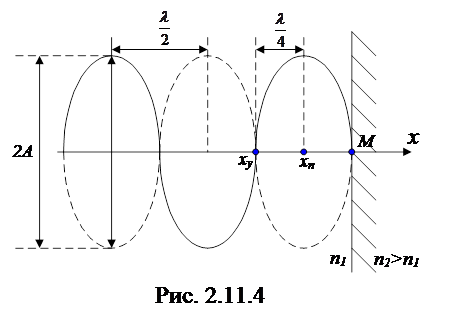 |
амплитуда колебаний достигает максимального значения (рис. 2.11.4).
Эти точки называют пучностями волны.
Из формулы (2.11.16) находим координаты пучностей:
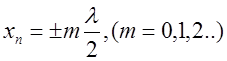 . (2.11.17)
. (2.11.17)
В точках, где
 , (2.11.18)
, (2.11.18)
амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны (рис. 2.11.14). Из (2.11.18) находим координаты узлов
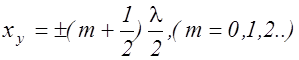 . (2.11.19)
. (2.11.19)
Из формул (2.11.17) и (2.11.19) следует, что расстояние между пучностями, так же как и расстояние между соседними узлами, равно 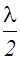 . Пучности и узлы сдвинуты друг относительно друга на четверть длины волны(рис.2.11.4).
. Пучности и узлы сдвинуты друг относительно друга на четверть длины волны(рис.2.11.4).
При отражении от более плотной среды, то есть когда n2>n1 (рис.2.11.4), происходит потеря полуволны и в точке отражения M возникает узел стоячей волны. Если n1> n2, то в точке образуется пучность. Стоячая волна не переносит энергию, так как образующие ее падающая и отраженная волны переносят энергию в равных количествах и в противоположных направлениях.
Рассмотренное явление следует учитывать при передаче высокочастотной энергии от передатчика к антенне посред-ством связывающих их фидерных устройств, в качестве которых используются двухпроводные линии, состоящие из длинных параллельных проводников, называемых линиями Лехера. Для передачи энергии в таком фидерном устройстве необходимо исключить возможность появления стоячей волны, что достигается согласованием антенны, фидера и выходных цепей передатчика по волновому сопротивлению. В этом случае не возникает отраженная волна от мест соединения и высокочастотная энергия с передатчика идет на антенное устройство и излучается в виде электромагнитных волн в пространство.
Стоячие волны получаются в резонаторах радиотехнических схем на высоких и сверхвысоких частотах, при этом добротность резонаторов значительно выше значений добротностей, достижимых в LC контурах.
Интерференция волн оптического и радиодиапазона с образованием стоячих волн является достаточно широко распространенным явлением и может играть как положительную, так и отрицательную роль.
§2.12. Интерференция в тонких пленках.
Просветление оптики
В тонких прозрачных пленках наблюдается интерференция света в результате наложения когерентных волн, отраженных от верхней и нижней поверхностей пленки. Этим явлением объясняется радужная окраска мыльных пленок, тонких пленок нефти или минерального масла, плавающих на поверхности воды, цвета побежалости на поверхности закаленных деталей, покрытых тончайшим прозрачным слоем окислов.
Для установления общих закономерностей интерференции света в тонких пленках рассмотрим плоскопараллельную прозрачную пластинку толщиной d с показателем преломления n, на которую под углом a падает плоская монохроматическая волна (рис. 2.12.1). Рассмотрим лучи
I и II, проведенные перпендикулярно фронту падающей волны АД. Луч 1, падающий на пластинку в точке A, частично отражается, а частично преломляется под углом b в пластинке.

|
В точке C он частично преломится в воздух и частично отразится и попадет в точку B. B этой точке луч вновь частично отражается и преломляется. В точке B луч 1 выйдет в воздух под углом a. Луч II падает в точку B под углом a и частично отражается под таким же углом. В результате в глаз наблюдателя попадает два луча: луч I, прошедший путь в пластинке AC+CB , и луч II, прошедший путь DB в воздухе и отраженный от пластинки в точке B. Оптическая разность хода лучей I и II равна
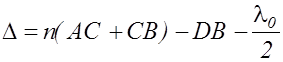 . (2.12.1)
. (2.12.1)
В выражении (2.12.1) учтено, что при отражении от более плотной среды луч II теряет половину длины волны в ваку-уме. Из рис. 2.12.1 следует, что
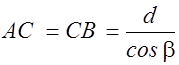 ;
; 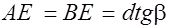 ;
;
DB=2d tgb sina.(2.12.2)
Подставляя (2.12.2) в (2.12.1) получаем
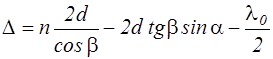 . (2.12.3)
. (2.12.3)
Из закона преломления следует, что
sina =n sinb.(2.12.4)
С учетом (2.12.4) выражение (2.12.3) принимает вид
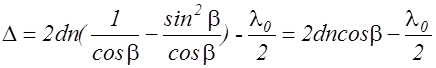 . (2.12.5)
. (2.12.5)
С помощью (2.12.4) оптическую разность хода волн можно выразить и через угол падения:
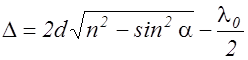 . (2.12.6)
. (2.12.6)
Если пленка находится не в воздухе, а в среде с показателем преломления n1¹1, то формула (2.12.6) преобразуется в следующую:
 , (2.12.7)
, (2.12.7)
где 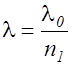 - длина волны в среде с показателем преломленияn1; n2 показатель преломления пленки.
- длина волны в среде с показателем преломленияn1; n2 показатель преломления пленки.
Результат интерференции лучей I и II зависит от значения D:
при D = ml0 (2.12.8)
наблюдается максимум интенсивности;
при 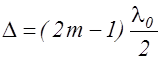 (2.12.9)
(2.12.9)
наблюдается минимум интенсивности.
Пленка в отраженном свете будет казаться светлой, если выполняется условие (2.12.8), и темной - при выполнении условия (2.12.9). Пленкам различной толщины соответствует и различная окраска.
На явлении интерференции света в тонких пленках основан метод просветления оптики, предложенный академиком И.В. Гребенщиковым. Этот метод позволяет устранить отражение света от поверхностей линз в оптических приборах (фотоаппаратах, биноклях, перископах и др.).
Специальной химической обработкой поверхностей линзы (выщелачивание стекла раствором кислот) создают на ней тонкую пленку толщиной 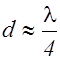 , показатель преломления которой несколько меньше показателя преломления стекла nСТ .
, показатель преломления которой несколько меньше показателя преломления стекла nСТ .  Толщина пленки подбирается такой, чтобы осуществлялся интерференционный минимум отражения для света с длиной волны
Толщина пленки подбирается такой, чтобы осуществлялся интерференционный минимум отражения для света с длиной волны
l » 5,5 10-7 м (ей соответствует наибольшая чувствительность глаза). Оптическая разность хода лучей 1 и 2 (рис. 2.12.2) равна D =2d nпл, а первый интерференционный минимум будет наблюдаться, если выполняется условие (2.12.9) при m=1 то есть:
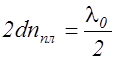 , (2.12.10)
, (2.12.10)
откуда толщина пленки равна
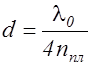 . (2.12.11)
. (2.12.11)
Такая оптика получила название просветленной. В отраженном свете просветленные линзы кажутся окрашенными в фиолетовый цвет, так они заметно отражают сине-фиолетовый свет.
Наиболее полное взаимное гашение волн, отраженных от верхней и нижней поверхностей пленки, происходит в случае равенства интенсивностей этих волн. Можно показать, что оптимальное значение nпл связано с показателем преломления стекла nCT соотношением:
 .
.
Метод, используемый для просветления оптики, применяется также для радиолокационной маскировки летящих объектов. Для этого объект покрывают тонкой пленкой толщиной примерно в четверть длины волны, излучаемой радиолокатором.
Дата добавления: 2015-07-24; просмотров: 2430;
