Дифракция Френеля от простейших преград
Расcчитаем дифракционную картину, которая получается, если на пути сферической волны поставить преграду с круглым отверстием радиуса r0 (рис. 2.15.1). Если радиус отверстия r0<< a,b, то а можно считать равным расстоянию от источника S до преграды, а b - расстоянию от преграды до точки P. Если расстояния a и b удовлетворяют условию
r0= 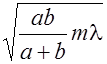 , (2.15.1)
, (2.15.1)
|
где m - целое число, то отверстие оставит открытыми m - первых зон Френеля, построенных для точки P. Из (2.15.1) находим число открытых зон Френеля:

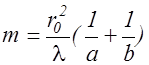 . (2.15.2)
. (2.15.2)
В соответствии с (2.14.11) амплитуда колебаний в точке Р будет равна
E p = E1 – E2 + E3 – E4 +... ±Em . (2.15.3)
В этом выражение у Em берется знак плюс, если m - нечетное, и знак минус, если m - четное.
Так как амплитуды от двух соседних зон почти не отличаются, то в результате суммирования амплитуду колебания в точке P можно представить в виде
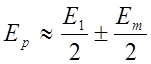 , (2.15.4)
, (2.15.4)
где плюс берется для нечетных m, а минус - для четных.
При малых m, Em мало отличается от E1. Следовательно, при нечетных m Ep » E1, а при четных Ep»0.
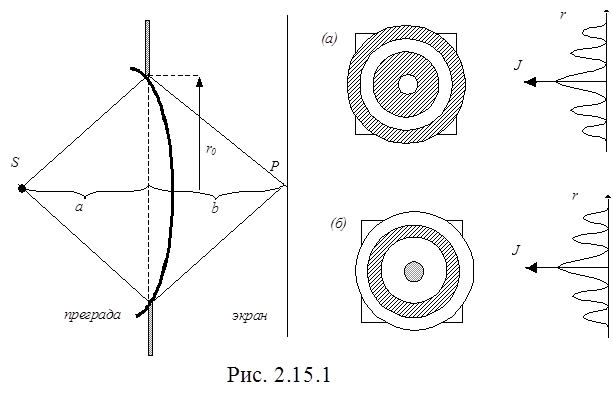
Если смещаться по экрану из точки P (рис.2.15), то интенсивность света будет изменяться, принимая минимальные и максимальные значения, так как для каждой точки экрана она определяется действием открытых участков четных и нечетных зон. Таким образом, дифракционная картина от круглого отверстия состоит из светлых и темных концентрических колец, причем при m - нечетном в центре - светлое пятно (рис. 2.15.1а), а при m - четном в центре - темное пятно(рис. 2.15.1б).
При перемещении экрана параллельно самому себе вдоль прямой SP картины, изображенные на рис. 2.15.1 а; б, будут сменять друг друга, так как в соответствии (2.15.2) m становится то четным, то нечетным.
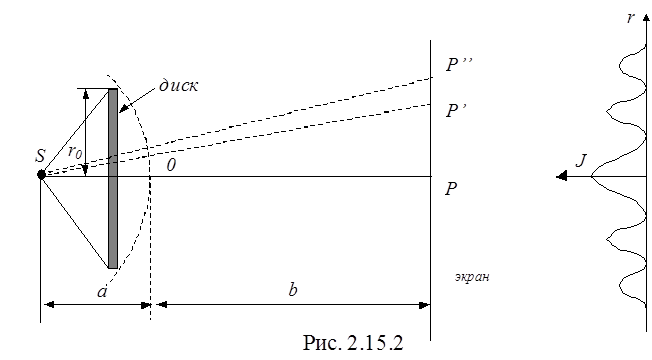
|
Поместим между точечным источником света S и точкой наблюдения P непрозрачный круглый диск радиуса r0
(рис. 2.15.2), который закрывает m - первых зон Френеля.
Тогда амплитуда световой волны в точке P будет равна
Ep=Em+1–Em+2 + Em+3 - ..= 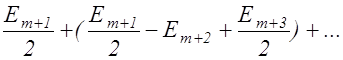 .
.
Дата добавления: 2015-07-24; просмотров: 1564;
