Векторная диаграмма зон Френеля. Зонные пластинки. Дифракция Френеля на простейших преградах.
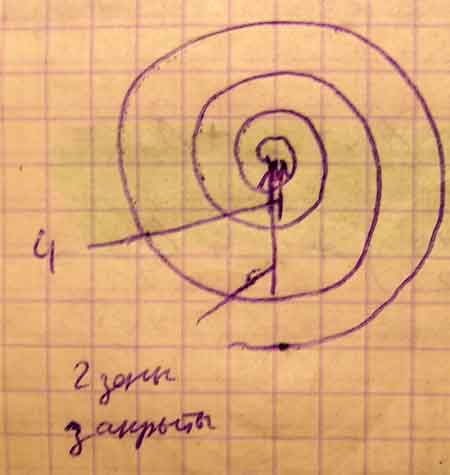
Рассмотрим векторную диаграмму зон Френеля. Она представляет собой спираль, а результирующий вектор А представляет собой вектор, соединяющих начало и конец.
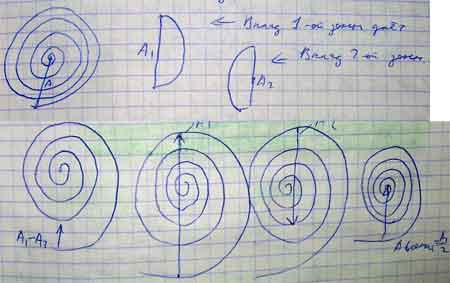
Если на пути сферической волны от точечного источника поставить прозрачную преграду, которая закрывала бы любые чётные, либо все нечётные зоны Френеля, то интенсивность в точке наблюдения очень усилилась.
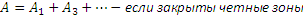
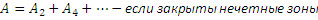
Такие пластины называются амплитудными зонами пластины. Если же прозрачные пластинки меняют фазу на Пи всех чётных или нечётных зон Френеля, то амплитуда и интенсивность света в точке наблюдения возрастёт в ещё большей степени, т.к. в этом случае
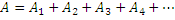
Также пластины называются фазовыми знаками пластинки. Зонные пластинки действуют подобно собирающим линзам, т.к. позволяют сформулировать и увеличить интенсивность точки.
Дифракция на круговом отверстии.
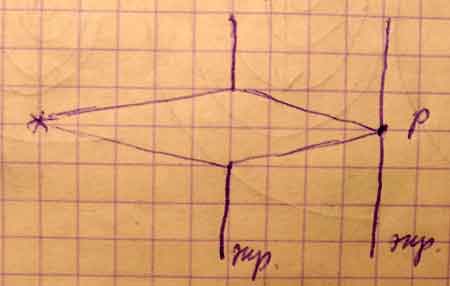
В центре дифракционной картины (в Р) будет наблюдаться тёмное пятно (минимум I), если в отверстии укладывается чётное число зон Френеля. Максимум наблюдается (светлое пятно), если в отверстии укладывается нечётное число зон.
Пусть n –чётное число, тогда 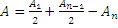
Если n=2, то 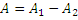 – мало.
– мало.
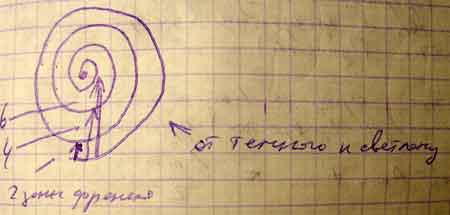
Пусть n – нечётное, тогда 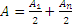 .
.
Если n=2, то 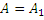 – большое.
– большое.

Дифракция на круговом диске.
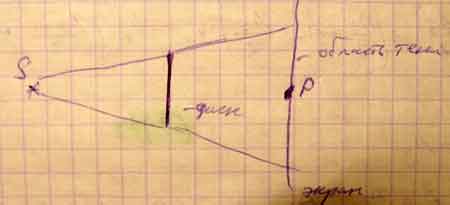
Особенностью дифракции сферических волн от точечного источника на непрозрачном диске является присутствие в центре геометрической тени светлого пятна (пятна Пуассона).
Амплитуда в данной точке определяется первой открытой зоной Френеля. Пусть m-число зон Френеля, тогда A= 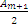
Дата добавления: 2015-08-14; просмотров: 1986;
