Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля.
Дифракция света – это совокупность явлений, заключающиеся в перераспределении светового потока при прохождении световой волны в средах с резкими неоднородностями. В узком смысле дифракция – это огибание волнами препятствие. Присутствие дифракции приводит к нарушению законов геометрии оптики, в частности – законов прямолинейного преломления.
Между дифракцией и интерференцией нет разницы, т.к. оба явления приводят к распределению световой волны. Различают дифракцию Фраунгофера и дифракцию Френеля.
Дифракция Фраунгофера – дифракция параллельных лучей. Наблюдается когда экран или точка наблюдения расположены далеко от препятствия, на котором наблюдается дифракция.
Дифракция Френеля – это дифракция сходящихся лучей. Наблюдается на близком расстоянии от препятствия.
Качественно явление дифракции объясняется принципом Гюйгенса: каждая точка фронта волны становит источником вторичных сферических волн, и фронт новой волны является огибающей этих вторичны волн. Принцип Гюйгенса качественно объяснял дифракцию, но не давал информацию об интенсивности дифрагированной волны в разных направлениях.
Френель дополнил принцип Гюйгенса идеей о когерентности и интерференция этих вторичных волн, что дало вторичным рассчитывать интенсивность волны разных направлений.
Принцип Гюйгенса-Френеля: каждая точка фронта волны становится источником когерентных вторичных сферических волн и новых фронт волны образуется в результате интерференции этих волн.
Метод зон Френеля. Френель показал, что в случаях, отличающихся симметрией волнового фронта или волновой поверхности их можно разбить на особые зоны, соседние из которых действуют противофазе в какой-либо точке пространства заменить алгебраическим сложением амплитуд, создаваемых в этой точке пространства данными законами. Рассмотрим построение для случая сферического фронта или волновой поверхности (такой фронт даёт точечный источник света).
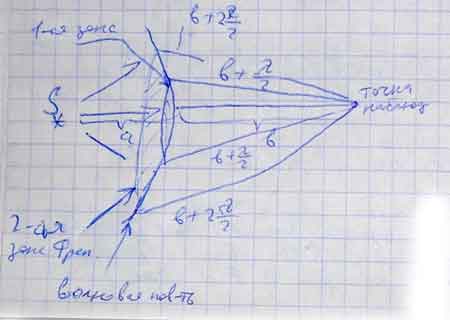
Френель предложил разбивать эту поверхность на зоны, расстояние от границ которых до точки наблюдения различаются на λ/2. Соседние зоны действуют в противофазе, т.е. амплитуды, создаваемые ими в точке наблюдения вычитаются. Найдём радиусы 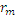 и площади
и площади 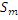 кольцевых зон Френеля для случая сферической волновой поверхности.
кольцевых зон Френеля для случая сферической волновой поверхности.
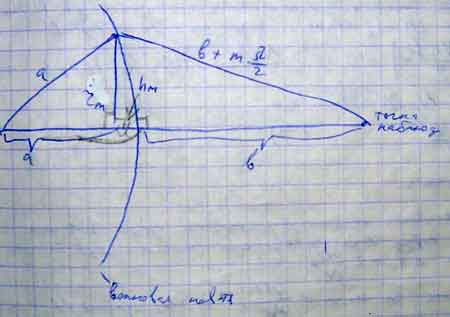
Из прямоугольных треугольников получим 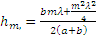 Для небольших m-
Для небольших m- 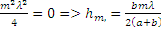 .
.
Из геометрии известно, что площадь сферического сегмента 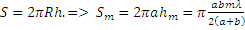 =>
=> 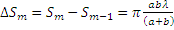 , т.е. не зависти от номера m => площади таких зон одинаковы.
, т.е. не зависти от номера m => площади таких зон одинаковы.
Из рисунка 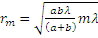 . Несмотря на то, что площадки зон Френеля в данном случае равны, амплитуда, создаваемая в каждой зоне в точке наблюдения уменьшается с ростом m, т.е.
. Несмотря на то, что площадки зон Френеля в данном случае равны, амплитуда, создаваемая в каждой зоне в точке наблюдения уменьшается с ростом m, т.е. 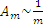 . Это связано с тем, что амплитуда для каждой зоны зависит от угла α между нормалью к этой зоне и направлением от этой зоны в точке наблюдения.
. Это связано с тем, что амплитуда для каждой зоны зависит от угла α между нормалью к этой зоне и направлением от этой зоны в точке наблюдения.

Приближенно считают, что A= 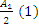 , т.к. считается, что амплитуда для какой-нибудь зоны является средней между двумя соседними зонами, т.е.
, т.к. считается, что амплитуда для какой-нибудь зоны является средней между двумя соседними зонами, т.е. 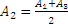 .
.
Т.к. 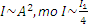 .
.
Дата добавления: 2015-08-14; просмотров: 1033;
