Полосы равной толщины, равного наклона, Кольца Ньютона.

Параметры d, α и λ₀ определяют интерференционную картину в исследуемой плёнке. Если зафиксировать d, то интерференционный max и min наблюдаются для определения углов падения α. Реализуются интерференционные полосы равного наклона. Они получаются, если расходящийся пучок света направить на плоско параллельную пластинку.

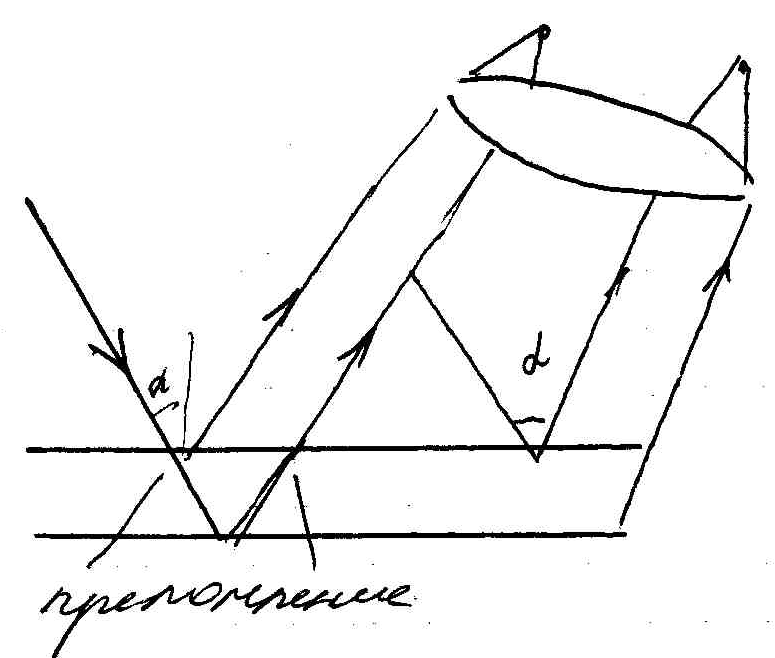
Полосы равного наклона локализованы на бесконечности (рис).

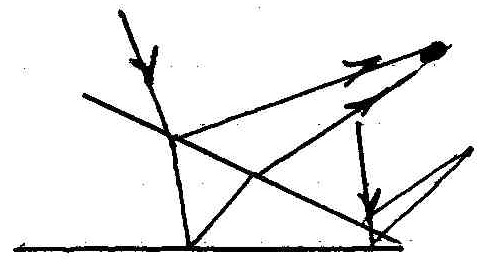
Если зафиксировать угол падения α и взять плёнку переменной толщины, то для определённых участков с толщиной d реализуются полосы равной толщины, которые можно получить, если направить параллельный пучок света на пластинку с разной толщиной в разных местах.

Рассмотрим классический пример полос равной толщины – кольца Ньютона. Они образуются, если на линзу, лежащую на стеклянной пластине направить монохроматический пучок света.

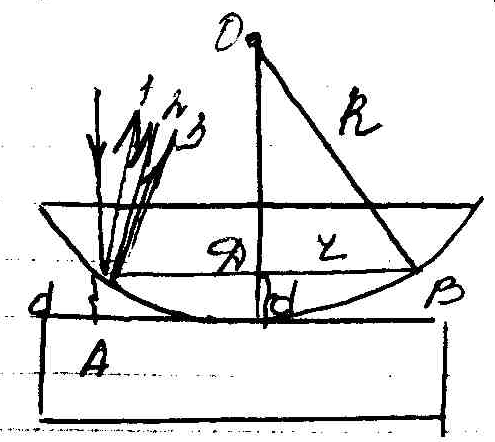
Луч 1 – некогерентный по отношению к лучам 2 и 3, т.к. для него не выполняется условие 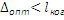=> когерентными являются лучи 2 и 3.

Разность хода между 2 и 3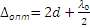

Найдём радиус колец Ньютона, которые соответствуют определённой ширине промежутка d.

Радиус тёмных колец в образовавшемся свете 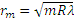., светлых - 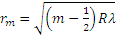=> в центре интерференционной картины будет тёмная точка. Кольца Ньютона можно наблюдать и в проходящем свете. В этом случае разность хода =2d.

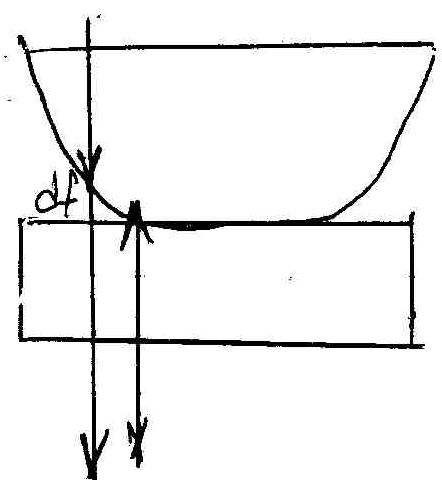
По этой причине при наблюдении колец Ньютона в проходящем свете, светлые и тёмные кольца меняются местами, т.е. 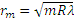- для тёмных, 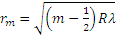- для светлых.