Дифракционная решетка. Если точка наблюдения (или источник) бесконечно удалена от преграды, то наблюдается дифракция в параллельных лучах

Если точка наблюдения (или источник) бесконечно удалена от преграды, то наблюдается дифракция в параллельных лучах. Дифракционная картина возникает в фокальной плоскости собирающей линзы, расположенной за преградой. Освещенность дифракционных максимумов при этом может быть гораздо больше, чем при дифракции Френеля. Рассчитаем дифракционную картину от узкой бесконечно длинной щели, на которую нормально падает плоская световая волна (рис. 2.16.1).

Ширина щели AB = b, длина l >> b. В соответствии с принципом Гюйгенса-Френеля точки щели являются источниками когерентных вторичных волн. Оптическая разность хода волн распространяющихся вдоль лучей AM и BN равна

D=BD=bsinj, (2.16.1)

где точка D - основание перпендикуляра, опущенного из точки A на луч BN.

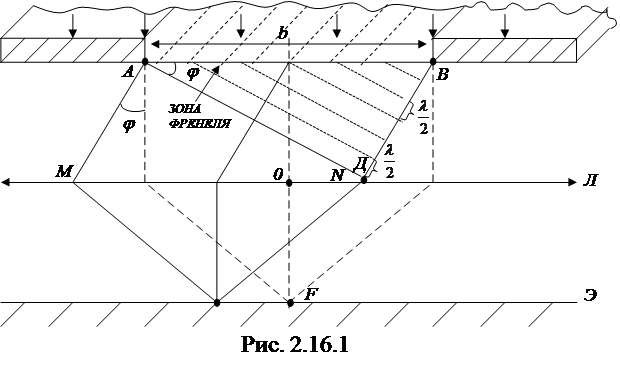Применим к плоскому фронту AB метод зон Френеля. Разобьем разность хода D(BD) на участки длиной 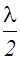, и из полученных точек проведем прямые, параллельные AD
(рис. 2.16.1).

Пересечение этих прямых с фронтом AB разбивает его по ширине на зоны Френеля, которые излучают свет в заданном направлении (под углом дифракции j) совершенно одинаково. При наложении волн в точке P от каждой пары соседних зон Френеля амплитуда результирующего колебания равна нулю, так как они возбуждают колебания с одинаковыми амплитудами и противоположными фазами. Таким образом, результат интерференции вторичных волн в точке P определяется тем, четное или нечетное число зон Френеля укладывается на щели.

Если число зон Френеля четное, то выполняется условие:

bsinj = ± 2k 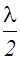(k = 1,2,3,4..), (2.16.2)

и в точке P наблюдается дифракционный минимум. Если число зон Френеля нечетное, то

bsinj = ±(2k + 1) 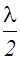(k = 1,2,3,4..), (2.16.3)

и в точке P наблюдается дифракционный максимум, соответствующий действию одной зоны Френеля.