При дифракции Френеля на экране получается дифракционное изображение препятствия, а при дифракции Фраунгофера - дифракционное изображение удаленного источника света.
Явление дифракции волн может быть объяснено качественно с помощью принципа Гюйгенса (§2.9).
Однако принцип Гюйгенса не позволяет оценить интенсивность волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем, который дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Поясним принцип Гюйгенса-Френеля на следующем примере. Пусть S на рис.2.13.1 одна из волновых поверхностей света, распространяющегося от некоторого источника.
|
Амплитуда колебаний вектора 
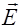в точке P может быть найдена из следующих соображений. Каждый элемент поверхности S является источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS. Учтем, что амплитуда сферической волны убывает по закону 
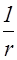(§2.2). Следовательно, волна, пришедшая от элемента dS в точку P, возбудит колебание:
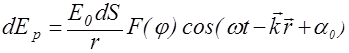. (2.13.1)
В этом выражении (wt+a0) - фаза колебаний на волновой поверхности S , k- волновое число, r -расстояние от элемента
dS до точки P, E0 - амплитуда колебания вектора 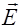в месте нахождения элемента dS. Коэффициент F(j)убывает при увеличении угла j между нормалью 
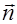к элементу dS и направлением на точку P и обращается в нуль при 
.
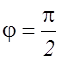Результирующее колебание в точке P представляет собой суперпозицию колебаний (2.13.1), взятых для всей волновой поверхности:
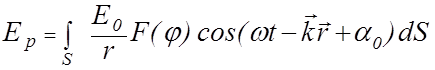. (2.13.2)
Формула (2.13.2) представляет собой аналитическое выражение принципа Гюйгенса-Френеля.
Дата добавления: 2015-07-24; просмотров: 776;