Величина k - называется порядком дифракционного максимума.

В направлении j = 0 наблюдается самый интенсивный центральный максимум нулевого порядка, так как в точке F (фокус линзы) все вторичные волны вызывают синфазные колебания. Распределение интенсивности на экране, полученное за счет дифракции световой волны, называется дифракционным спектром (рис.2.16.2).

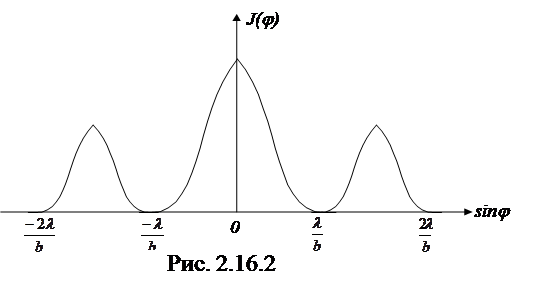
Количество минимумов на дифракционной картине найдем из условия (2.16.2)

k = .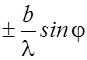

Так, как 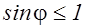, то k .

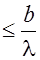При наблюдении дифракции от щели в белом свете, дифракционная картина становится окрашенной. В дифракционном максимуме каждого порядка ближе к центральному максимуму расположены максимумы, соответствующие меньшим длинам волн (формула 2.16.3).

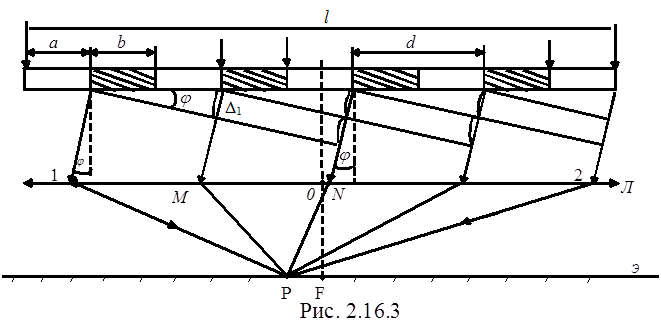
Система многих параллельных щелей, разделенных непрозрачными промежутками, называется дифракционной решеткой. На принципе дифракционной решетки построены многие антенны, состоящие из нескольких параллельных когерентных излучателей. Каждый излучатель играет роль одной щели.Пусть плоская световая волна падает на дифракционную решетку из N параллельных щелей шириной b каждая, расположенных на расстояниях b друг от друга (рис. 2.16.3).

Величина d = a + b называется постоянной (периодом) дифракционной решетки. Если ширина решетки l, то число щелей равно

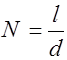. (2.16.4)

По принципу Гюйгенса-Френеля каждая щель является источником вторичных когерентных волн, способных интерферировать друг с другом. Разность хода волн, распространяющихся по лучам 1 и 2, равна

D=lsinj. (2.16.5)

Разность хода волн D₁ , идущих под углом j от двух соседних щелей, связанна с D соотношением

D=ND₁. (2.16.6)

Для волн, идущих от соседних щелей, условие максимумов имеет вид:

D₁=± kl, k = 0,1,2,3… .(2.16.7)

С учетом (2.16.7) выражение (2.16.6) принимает вид

D = ± N kl. (2.16.8)

Подставляя выражения (2.16.4) и (2.16.5), находим условие главных максимумов для решетки

dsinj=±kl, (2.16.9)

где k = 0,1.2.3 ... называют порядком главного максимума (или порядком спектра).

Амплитуда результирующего колебания в главных максимумах равна

E_M = NE₁ , (2.16.10)

где E₁ - амплитуда колебаний, созданных одной щелью.

С учетом (2.16.10) находим интенсивность главных максимумов:

J_max = N²J₁. (2.16.11)

Интенсивности главных максимумoв неодинаковы между собой из-за интерференции волн внутри каждого из пучков.

Главные минимумы наблюдаются для тех направлений, которые дают минимум для одной щели, то есть

bsinj=± kl, (k = 0,1,2,3... ). (2.16.12)

Кроме главных минимумов, в промежутках между соседними главными максимумами имеются (N – 1) добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания, созданные волнами от соседних щелей погашают друг друга. Они определяются условием

dsinj =± 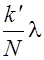, (2.16.13)

где 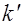= 1,2,... ( N-1 ),( N + 1),( 2N - 1),( 2N + 1).

В формуле (2.16.13) k' принимает все целочисленные значения, кроме 0, N, 2N, которые переводят условие (2.16.13) в условие главных максимумов (2.16.9).

Между дополнительными минимумами располагаются слабые вторичные максимумы. Между соседними главными максимумами число таких вторичных максимумов равно N -2.

График функции J(sinj) представлен на рис. 2.16.4.

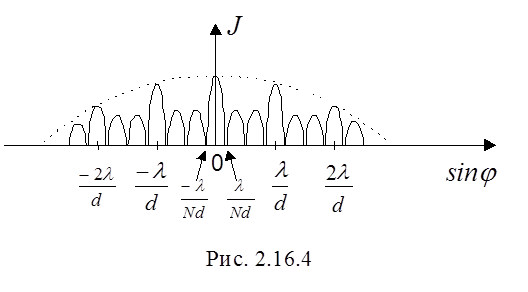
Если дифракционная решетка освещается белым светом, то для разных l положения главных максимумов, кроме центрального (k=0), не совпадают друг с другом.

Поэтому центральный максимум имеет вид белой полоски, а все остальные - радужных полосок, называемых дифракционными спектрами первого, второго и так далее порядков. В пределах каждой полоски окраска изменяется от фиолетовой у внутреннего края(ближайшего к максимуму нулевого порядка) до красной - у наружного края.

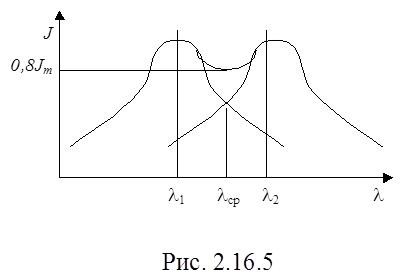
Одной из основных характеристик спектрального прибора является его разрешающая способность R, которая характеризует возможность раздельной регистрации двух близких спектральных линий. Согласно критерию, предложенному Рэлеем, спектральные линии считаются полностью разрешенными, если середина одного максимума совпадает с краем другого(рис. 2.16.5).

В этом случае минимум между линиями составляет 80% от максимума.Для дифракционной решетки разрешающая способность оценивается по формуле

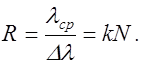(2.16.14)

Дифракция электромагнитных волн радиодиапазона учитывается не только в прокладке линий связи, но и в конструировании антенной техники и другой аппаратуры.

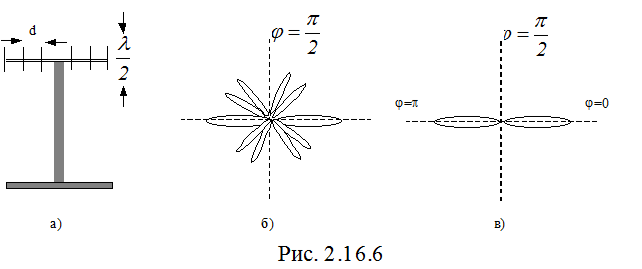
Для создания коротковолновых линий связи и для радиолокационных станций дальнего обнаружения необходимо сформировать остронаправленное радиоизлучение, сконцентрировав энергию передатчика в малом телесном угле. С этой целью применяют многоэлементные синфазные антенны (например многовибраторные, представляющие собой линейные решетки из полуволновых вибраторов). Если расположить излучатели радиоволн в ряд на одинаковых расстояниях d между ними и обеспечить равенство частоты, амплитуды и токов в вибраторах, то линейная цепочка вибраторов будет "работать" аналогично дифракционной решетке (рис. 2.16.6, а).

Диаграмма направленности такой решетки в экваториальной плоскости (перпендикулярной к вибраторам и проходящей через их середины) в достаточно удаленной точке наблюдения представляет собой систему узких главных максимумов, число которых зависит от соотношения 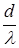. Из условия максимума дифракционной решетки d sinj= ±kl следует, что число максимумов

k≤ 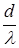, т.к. sinφ≤l.

На рисунке 2.16.6 изображена диаграмма наравленности для антенны с d=3,5λ. Если сделать антенну с d<λ (например, d=0,5λ), то в диаграмме направленности будут присутствовать только максимумы нулевого порядка (рис. 2.16.6, в), в которых будет сосредоточена вся энергия излучения.

Для получения излучения только в одном направлении, что особенно важно для дальней связи и радиолокации, антенну делают в виде сдвоенных решеток вибраторов, расстояние между которыми 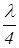, а токи сдвинуты на 90⁰. Период каждой решетки d по-прежнему составляет 0,5λ.