Метод зон Френеля

Найдем амплитуду колебания вектора 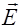в точке P, созданного сферической волной, распространяющейся в однородной среде от источника N (рис.2.14.1).

Волновая поверхность симметрична относительно прямой NP. Воспользовавшись этим Френель разбил волновую поверхность на кольцевые зоны так, что расстояния от краев каждой зоны до точки P отличаются на 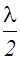.Расстояние b_m от края m^-ой зоны до точки P можно представить в виде

b_m=b+m 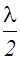, (2.14.1)

где b - расстояние от вершины волновой поверхности О до точки P.

Так как разность хода волн, приходящих в точку P от аналогичных точек двух соседних зон, равна 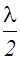, то созданные ими колебания будут находиться в противофазе.

Для оценки амплитуд колебаний найдем площади зон Френеля. Внешняя граница m^-ой зоны выделяет на волновой поверхности сферический сегмент высоты h_m (рис. 2.14.2).

Обозначим площадь этого сегмента S_m. Площадь m^-ой зоны можно представить в виде

D S_m = S_m- S_m-1, (2.14.2)

где S_m-1 - площадь сферического сегмента, выделяемого внешней границей (m-1)^-й зоны. Из рис.2.14.2 следует, что

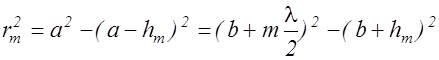, (2.14.3)

где a - радиус волновой поверхности, r_m- радиус внешней границы m^-ой - зоны. Возводя в квадрат скобки в (2.14.3), получим

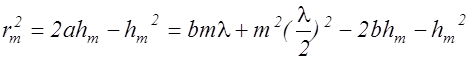, (2.14.4)

откуда

. (2.14.5)

При не слишком больших m, ввиду малости l выражение (2.14.15) можно представить в виде

. (2.14.6)

Находим площадь сферического сегмента высотой h_m и радиусом a:

. (2.14.7)

Площадь m^-ой - зоны Френеля находим по формуле (2.14.2) с учетом формулы (2.14.7)

. (2.14.8)

Так как в выражение (2.14.8) m не входит, то это означает, что при не слишком больших m площади зон Френеля примерно одинаковы.

Оценим радиусы зон Френеля. Учтем, что при не слишком больших m h_m<< a, поэтому из формулы (2.14.4) находим

. (2.14.9)

Подставляя в (2.14.9) h_m согласно формуле (2.14.6), находим радиус внешней границы m^-й - зоны Френеля:

. (2.14.10)

Если в формуле (2.14.10) положить a=b=1м и l=0,5 мкм то для радиуса центральной (первой) зоны Френеля получим значение r₁= 0,5 мм.

Поскольку площади зон Френеля примерно одинаковы, расстояние b_m медленно растет с увеличением m, а F(j) -убывает с ростом m, то амплитуды E_m колебаний, созданных зонами Френеля в точке P,будут монотонно убывать с ростом m:

E₁> E₂...> E_m-1>Е_т>E_m+1>….

Фазы колебаний, возбуждаемых соседними зонами, отличаются на p. Поэтому амплитуда результирующего колебания в точке P может быть найдена алгебраическим суммированием знакопеременного ряда

E _рез =E₁- E₂+ E₃-E₄+... (2.14.11)

Перепишем (2.14.11) в виде

(2.14.12)

Вследствие монотонности убывания E_m можно приближенно считать, что

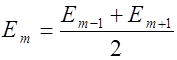. (2.14.13)

С учетом (2.14.13) выражение (2.14.12) примет вид

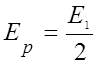. (2.14.14)

Из (2.14.14) следует, что действие всей волновой поверхности эквивалентно половине действия центральной зоны (ранее отмечалось, что r₁=0,5 мм для l=0,5 мкм), то есть свет от точки N до точки P распространяется как бы в пределах узкого канала, что соответствует представлению о прямолинейности распространения света.