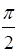Называется относительным показателем преломления второй среды по отношению к первой.

Если первая среда вакуум, в котором фазовая скорость электромагнитных волн равна c, то отношение

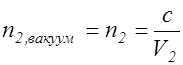(2.9.4 )

называютабсолютным показателем преломления cреды 2.

Относительный показатель преломления двух сред равен отношению абсолютных показателей преломления этих сред. Действительно, учитывая (2.9.4), получим:

^{, ,}

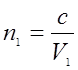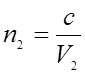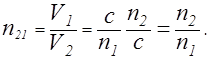2.9.5

Учитывая, что в теории Максвелла для фазовой скорости электромагнитной волны получено выражение

^,

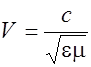для абсолютного коэффициента преломления среды получим формулу

n = 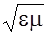. (2.9.6)

Для прозрачных сред m » 1, поэтому

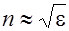. (2.9.7)

Показатель преломления любой среды n зависит от ее состояния (плотности и температуры) и частоты электромагнитной волны.

Из закона преломления волн, записанного в виде

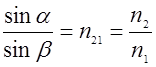^, (2.9.8)

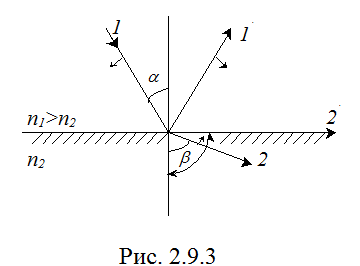
следует, что при переходе волны через границу раздела двух сред, для которых n₂ > n₁, преломленный луч приближается к нормали. При обратном соотношении показателей преломления n₁>n₂ преломленный луч удаляется от нормали. Среда с большим показателем преломления называется оптически более плотной. Рассмотрим случай падения волны на границу с оптически менее плотной средой (рис. 2.9.3).

С увеличением угла падения a будет расти и угол b. Так как b>a, то при некотором значении a_пред. преломления луч 2 будет направлен вдоль границы раздела (b 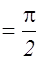). Значение предельного угла определяется из (2.9.8):

sina_пред 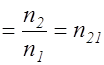. (2.9.10)

При углах падения, больших sina_пред, преломленного луча не будет, останется лишь отраженный луч. Формально это следует из того, что при углах падения a>a_предиз (2.9.8) для sinb получаются значения, большие единицы, что, очевидно, невозможно.

Описанное выше явление носит название полного внутреннего отражения. Явление полного внутреннего отражения используется в различных оптических приборах (бинокли, перископы) и лежит в основе оптических волноводов, которые представляют собой волокна из прозрачного материала (кварц) (рис. 2.9.4).

Лучи света в оптических волноводах падают на стенку волокна под углами a > a_пред..

Вопросами переноса световой энергии по оптическим волокнам занимается специальный раздел оптики - так называемая “волоконная оптика”.

Волоконные световоды нашли широкое применение в системах оптической связи, позволяя передавать очень большой объем информации на значительные расстояния. Отдельные волокна могут объединяться в жгуты и кабели, увеличивая таким образом объем передаваемой информации. Технические характеристики оптических кабелей для абонентских, внутриузловых и магистральных линий позволяют им конкурировать с обыкновенными проводными линиями связи, в перспективе вытесняя их.

§2.10. Монохроматичность. Принципы суперпозиции волн. Когерентность

Монохроматическим называется электромагнитное излучение одной постоянной частоты. Опыт показывает, что при распространении в среде нескольких электромагнитных волн, каждая из них движется независимо от других. Так, например, распространяются радиоволны от двух или нескольких радиостанций, световые волны от нескольких источников света. Поскольку волны не взаимодействуют между собой, то каждая область пространства, в которой распространяются несколько волн, будет принимать участие в колебаниях, вызванных каждой волной в отдельности.

Для того, чтобы найти результирующее колебание в данной точке пространства, необходимо воспользоваться принципом суперпозиции волн. Для электромагнитных волн этот принцип сводится к принципу суперпозиции электрических и магнитных полей. Так, например, результирующее электрическое поле, созданное в некоторой точке наложения нескольких электромагнитных волн, будет иметь напряженность

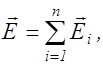(2.10.1)

где 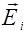- вектор напряженности электрического поля, созданного в рассматриваемой точке i-ой электромагнитной волной.

Аналогично для вектора напряженности магнитного поля

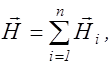(2.10.2)

где 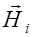- вектор напряженности магнитного поля i-ой волны.

Принцип суперпозиции применим только к волнам малой интенсивности - звуковым, радиоволнам, световым от обычных источников. К ударным волнам, а также к высокоинтенсивному лазерному излучению он не применим, так как под воздействием излучения большой интенсивности изменяются оптические характеристики среды.

Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями вектора напряженности электрического поля. По этой причине в дальнейшем о векторе напряженности магнитного поля упоминать не будем.

Рассмотрим две монохроматические электромагнитные волны одинаковой частоты, которые, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания напряженности электрического поля одинакового направления:

E₁ = E_m1cos(wt + a₁),

E₂ = E_m2cos(wt + a₂). (2.10.3)

Амплитуда результирующего колебания в данной точке определяется (Глава I) формулой

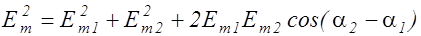. (2.10.4)

Если разность фаз a₂ - a₁ возбуждаемых волнами колебаний остается постоянной во времени, то волны называются когерентными. Источники таких волн также называются когерентными.

В случае наложения некогеретных волн разность фаз непрерывно меняется со временем,принимая равновероятно любые значения от 0 до 2p, вследствие чего среднее по времени значение <cos(a₂ - a₁)>_t равно нулю. В этом случае, усредняя (2.10.4) по времени, получим

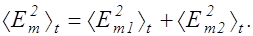(2.10.5)

Приняв во внимание, что интенсивность электромагнитной волны пропорциональна квадрату амплитуды вектора напряженности (формула 2.4.16) из (2.10.5) получим

J = J₁ + J₂. (2.10.6)

Из повседневного опыта известно, что при освещении какой-либо поверхности несколькими источниками света (например, двумя лампочками) освещенность поверхности описывается формулой (2.10.6) и монотонно убывает по мере удаления от источников света. Этот результат объясняется тем, что естественные источники света некогерентны. Излучение светящегося тела слагается из волн, испускаемых атомами. Излучение атома продолжается около
10^-8 секунды. За это время успевает образоваться цуг волн длиной около 3 метров. Через некоторое время атом излучает вновь. Однако фаза нового цуга волн никак не связана с фазой предыдущего. Возбуждаемые большим количеством атомов волны, налагаясь друг на друга, образуют испускаемую телом волну, в которой фаза претерпевает случайные изменения во времени.

§2.11. Интерференция волн. Расчет интерференционной картины от двух когерентных источников.

Стоячие волны

При наложении когерентных волн cos(a₂ - a₁) имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому, переходя к интенсивностям в (2.10.4), получим

J = J₁ + J₂ +2 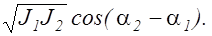(2.11.1)

В тех точках пространства, для которых cos(a₂ - a₁)>0,

J >J₁+J₂; в точках, для которых cos(a₂ - a₁) < 0, J<J₁+J₂.

Таким образом, при наложении когерентных волн происходит перераспределение интенсивности в пространстве, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности. Это явление называется интерференцией волн.

Когерентные световые волны можно получить, разделив(с помощью отражения или преломления) волну, излучаемую одним источником, на две части. Если эти волны пройдут разные оптические пути(произведение геометрической длины пути l на показатель преломления cреды, т.е. L = nl), затем наложатся друг на друга, то будет наблюдаться интерференция.

Разность оптических длин путей, проходимых интерферирующими волнами, должна быть меньше ~ 3 м, так как в противном случае наложатся волны, соответствующие разным цугам.

Получим условия интерференционных максимумов и минимумов. Пусть разделение монохроматической волны на две происходит в точке 0 (рис.2.11.1).

До точки P первая волна проходит путь l₁ в среде с показателем преломления n₁, вторая волна проходит путь l₂ в среде с показателем преломления n₂. Пусть исходная волна в точке P создает колебания, фаза которых равна wt, тогда первая волна в точке P возбудит колебание

E₁(t)=E_m1cosw(t - 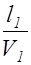), (2.11.2)

а вторая волна - колебание

E ₂(t)=E_m2cosw(t - 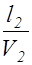), (2.11.3)

где 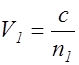,а 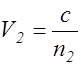- фазовые скорости волн.

Следовательно, разность фаз колебаний, возбуждаемых волнами в точке P, будет равна

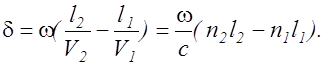(2.11.4)

Заменим в (2.11.4) 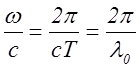, где l₀ - длина волны в вакууме. Выражение (2.11.4) можно записать в виде

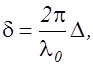(2.11.5)

где D = n₂l₂ - n₁l₁ = L₂ – L₁. (2.11.6)