Эффект Доплера. Пусть в упругой среде на некотором расстоянии от источника волн располагается устройство, воспринимающее колебания среды - приемник (рис

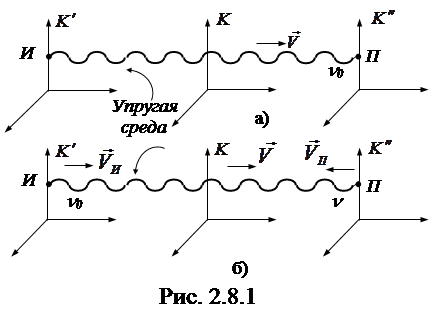Пусть в упругой среде на некотором расстоянии от источника волн располагается устройство, воспринимающее колебания среды - приемник (рис. 2.8.1, а).

Свяжем со средой, источником и приемником, соответственно, системы отсчета k, 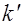и .

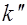Обозначим скорость распространения волны относительно среды V (скорость в системе k). Когда источник и приемник волн неподвижныотносительно упругой среды, то частота n колебаний, воспринимаемых приемником, будет равна частоте колебаний источникаn₀. Если же источник или приемник, либо оба они движутся относительно среды (рис. 2.8.1, б), то частота n, воспринимаемая приемником, отличается от n_0. Этот эффект открыт в 1842 году австрийским физиком К. Доплером.

Получим соотношение частот n и n₀ для случая, когда приемник и источник движутся вдоль соединяющей их прямой (рис. 2.8.1). Скорость источника V_и будем считать положительной, если источник движется по направлению к приемнику, и отрицательной, если источник удаляется от приемника. Аналогично скорость приемника V_п будем считать положительной, если приемник приближается к источнику, и отрицательной, если приемник удаляется от источника.

Скорость волны в системе 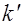(рис. 2.8.1, б) равна

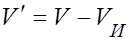. (2.8.1)

Длину волны находим из соотношения

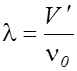^. (2.8.2)

Скорость волны в системе 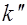равна

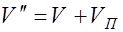. (2.8.3)

Частоту колебаний, воспринимаемых приемником, находим из соотношения

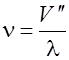. 2.8.4)

Подставим l из (2.8.2) в (2.8.4) и учтем (2.8.1) и (2.8.3), тогда получим

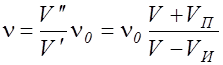. (2.8.5)

Формула (2.8.5) описывает увеличение воспринимаемой частоты колебаний при сближении источника и приемника. При удалении источника и приемника у V_П и V_И изменяются знаки и формула (2.8.5) переходит в следующую формулу, описывающую уменьшение воспринимаемой приемником частоты:

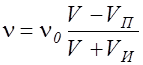^. (2.8.6)

Когда направление движения источника и приемника не совпадает с направлением соединяющей их прямой, в формулах (2.8.5) и (2.8.6) вместо VП и VИ необходимо взять их проекции на направление указанной прямой.

Эффект Доплера существует также для электромагнитных волн. Поскольку особой среды, являющейся носителем электромагнитных волн, не существует, то доплеровское изменение частоты электромагнитных волн определяется только относительной скоростью источника и приемника.

Свяжем с приемником ЭМВ начало координат системы k, а с источником - начало координат системы 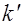(рис. 2.8.2).

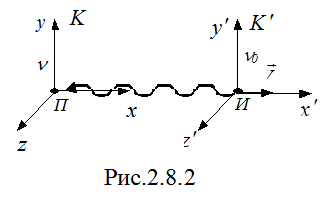
Пусть источник движется со скоростью 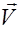относительно приемника. Запишем в системе 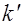уравнение плоской световой волны, испускаемой источником по направлению к приемнику

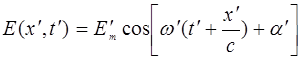, (2.8.7)

где w^' - частота колебаний источника, a^'- начальная фаза колебаний, c - скорость ЭМВ, которая одинакова во всех ИСО.

Согласно принципу относительности Эйнштейна все физические явления протекают одинаково во всех ИСО и, следовательно, ЭМВ в системе k должна описываться таким же уравнением, как и (2.8.7), то есть

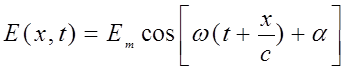. (2.8.8)

Уравнение (2.8.8) можно получить из уравнения (2.8.7), если с помощью преобразований Лоренца перейти от 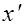и 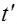к x и t.

Выполняя эти преобразования с (2.8.7) можно получить уравнение

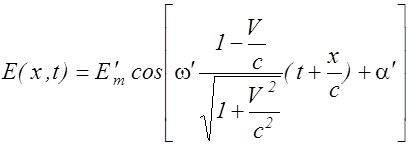. (2.8.9)

Уравнение (2.8.9) описывает ту же волну, что и уравнение (2.8.8). Поэтому должно выполняться соотношение:

(2.8.10)

Переходя от циклической частоты w к частоте n и обозначая частоту n' в системе источника через n₀, получим

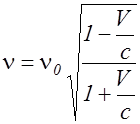. (2.8.11)

Скорость V источника по отношению к приемнику - величина алгебраическая. При удалении источника V> 0 и согласно (2.8.11) n <n0; при приближении источника к приемнику V< 0 и n >n0.

В случае, если V << c, можно показать, что формула (2.8.11) переходит в следующую:

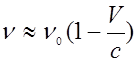^. (2.8.12)

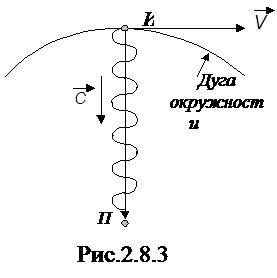
Соответствующий расчет показывает, что частота в системе приемника связана с частотой в системе источника соотношением

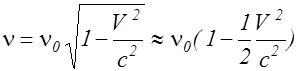. (2.8.13)

Так, в астрофизике эффект Доплера используется для определения скорости движения звезд и скорости вращения небесных тел. В радио- и гидролокации эффектДоплера используется для измерения скорости движущихся целей.

C эффектом Доплера приходится считаться при организации радиосвязи с быстролетящими объектами. Как следует из 2.7.3. информация в амплитудно-модулированном сигнале содержится лишь в одной боковой полосе, по этому для передачи можно использовать только одну из этих полос (с однополосно модулированным сигналом). Но чтобы восстановить в приемнике информационный сигнал, требуется точное знание частоты w, поскольку (w+d)-w=w-(w-d) =d.

Если предположить, что в приемнике зафиксирована частота w, а принимаемый сигнал отличается от преданного вследствие эффекта Доплера на величину Dw, т.е принимается сигнал с частотой w+d±Dw, то получаем
(w+d±Dw)-w=d±Dw. Поэтому в состав однополосно модулированного сигнала вводится остаток несущего колебания (пилот сигнал), с помощью которого корректируется частота w, в приемнике, таким образом, чтобы учесть ±Dw, получаем:

(w+d±Dw)-(w±Dw)=d.