Звуковая волна. Параметры звукового поля.

Волна называется бегущей, если обратная волна отсутствует. Пример распространения плоской бегущей волны представлен на рисунке 2.1 Стоячей называется волна, если она образована наложением двух одинаковых волн — прямой .и обратной, движущихся в про­тивоположных направлениях. Отношение звукового давления к колебательной скорости в плоской бегущей волне не зависит от амплитуды колебаний и называется волновым сопротивлением среды:

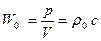(2.8)

В техниче­ской системе единиц при нормальных атмосферных условиях (t = 20° С, Р₀= 10 330 кГ/м²) волновое сопротивление W₀ = = 42 кГ сек/м³, в системе СИ W₀ = 420 н сек/м². В бегущей вол­не скорость и давление отличаются лишь масштабом - увеличе­нию давления соответствует увеличение колебательной скорости, и наоборот, скоростям частиц в отрицательном направлении соответствуют разрежения.

Изменение плотности в бегущей волне равно:

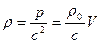(2.9)

Бегущая волна переносит энергию в направлении своего дви­жения. Средний поток энергии в какой-либо точке среды в единицу времени, отнесенный к единице поверхности, нормальной к .на­правлению распространения звука, называется интенсивностью звука в данной точке:

I = lim 1/T 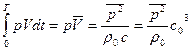, (2.10)

где черта означает осреднение во времени t; V ~ колебательная скорость частиц в звуковой волне. Интенсивность измеряется либо в кГм/см² или кГ/с м, либо в системе СИ в вт!м².

Интенсивность звуков, с которыми приходится иметь дело в практике борьбы с шумами, изменяется в очень широких пре­делах. Поэтому введена логарифмическая величина - уровень интенсивности звука

L_i = 10lg 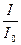, дБ (2.11)

Где I₀ = 10^-12 вт/м² = 10^-13 кГм/см² называется пороговой. В практике борьбы с современными шу­мами приходится иметь дело с уровнями интенсивности, лежа­щими в диапазоне от 20 до 170 дБ (т. е. диапазон изменения ин­тенсивности составляет 10¹⁵).

Человеческое ухо и многие акустические приборы чувстви­тельны не к интенсивности, а к среднему квадрату звукового давления. Поэтому введена величина уровня звукового давления

L_р = 10 lg 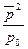= 20 lg 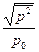, дБ (2.12)

где пороговое звуковое давление р₀ выбрано таким образом, что при нормальных атмосферных условиях

I₀ = 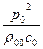(2.13)

где 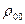и c₀ — плотность и скорость звука при нормальных ат­мосферных условиях. Тогда

p₀ = 2 10^-4дин/см² = 2 10^-5 н/м² = 2 10^-4 кГ/м²

Связь между уровнем интенсивности и уровнем звукового давления можно получить, разделив уравнение (2.10) на (2.13):

=

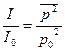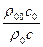
Прологарифмировав последнее соотношение, получим соотношение между уровнем интенсивности и уровнем звукового давления:

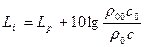(2.15)

При нормальных атмосферных условиях L_j = L_р.

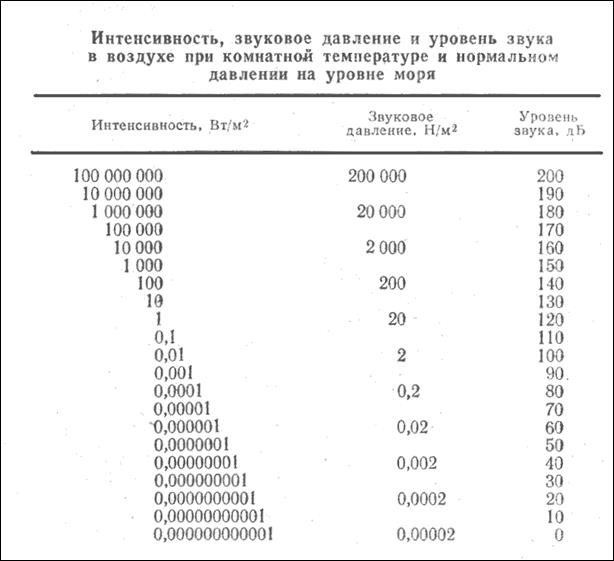
В таблице рассмотрено соотношение между интенсивностью звука, величиной звукового давления и уровня звукового давления.

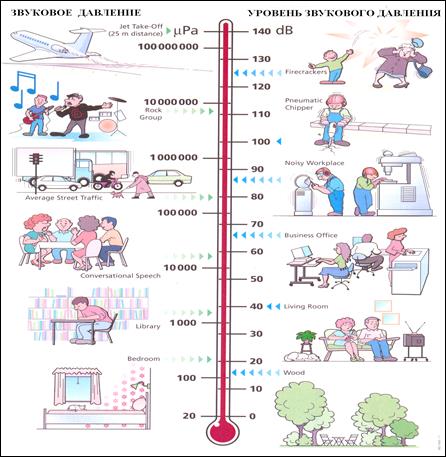
В простейшем случае физические параметры в звуковой вол­не меняются по закону косинуса (или синуса)

(2.16)

где р_m- амплитуда (р здесь не только звуковое давление, но и плотность, колебательная скорость, потенциал); ω—круговая частота; t - время. Такой звук называется чистым тоном.

Круговая частота связана с обычной частотой f , то есть с. числом полных колебаний в сек, измеряемым в герцах (гц] соотноше­нием

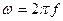(2.17)

Как известно, в комплексных величинах

.

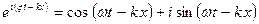Обозначив 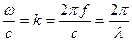, где к — волновое число; λ = с / f - длина звуковой волны, то есть расстояние между сосед­ними максимумами звукового давления, и применив комплексные обозначения, получим уравнение рас­пространения прямой плоской волны в комплексной форме:

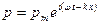, (2.18)

где 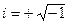- мнимая единица. Действительная часть выражения (2.18) соответствует выра­жению (2.16). Вместо (2.18) можно написать

.

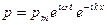Выражения е^iωt и е^-ikxназываются соответственно времен­ным и фазовым множителями. Физические характеристики синусоидальных звуковых волн выражаются с помощью следующих соотношений.

Звуковое давление:

;

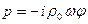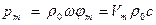; (2.19)

.

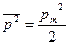Колебательная скорость:

;

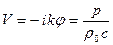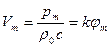; (2.20)

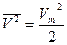
Интенсивность звука:

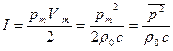(2.21)

Пример. Определить физические характеристики бегущей плоской синусо­идальной волны, соответствующей звуку с уровнем интенсивности L_i = 160 дБпри нормальных атмосферных условиях.

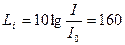дБ, откуда 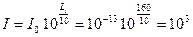кГм/с∙м².

Амплитуда звукового давления (2.19): 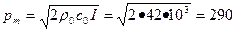кГ/м²;

Амплитуда колебательной скорости (2.20): ; м/с

Относительная ампли­туда изменения плотности .

На примере видно, что даже при очень высоких уровнях ин­тенсивности колебательные скорости малы по сравнению со ско­ростью звука, звуковые давления малы по сравнению с атмос­ферным давлением, а изменения плотности в волне очень неве­лики по сравнению с плотностью атмосферы.

Плотность звуковой энергии Е определяется количеством энергии в единице объема. В технической системе единиц размерность [Е] обозначается кГм/м³ или кГ/м², в СИ - дж/м³.

Скорость переноса энергии звуковой волны в неподвижной атмосфере равна скорости распространения звука с. Интенсив­ность звука в плоской бегущей волне можно представить как произведение плотности энергии Е на скорость ее переноса с: I = Еc, откуда

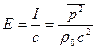(2.22)

Плотность звуковой энергии есть величина скалярная; она лучше характеризует энергию поля, чем интенсивность в тех слу­чаях, когда направление звука является неопределенным, напри­мер, в закрытых помещениях.

Звуковая волна при распространении переносит не только энергию, но и импульс. Другими словами, она оказывает давле­ние на предметы, находящиеся в звуковом поле. Это давление радиации обычно весьма невелико, но при высоких интенсивностях может стать заметным.

Наличие давления радиации исполь­зуется для измерения интенсивности в сильных звуковых полях. Оно представляет собой эффект второго порядка малости по от­ношению к звуковому давлению и обусловлено преимущественно наличием квадратов скоростей в уравнениях движения, отбрасы­ваемых при выводе уравнения акустики.

Величину давления радиации впервые определил Релей. Она зависит от поглощающих свойств площадки, на которую падает звуковой луч, от ориентировки этой площадки и ее размеров. В очень важном случае нормального падения плоской волны на твердую непоглощающую стенку бесконечных размеров давле­ние радиации равно:

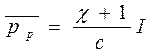(2.23)