Спектральные и временные характеристики
Отклонение физической величины р(t) в звуковой волне от состояния покоя может быть определено для каждого момента времени (детерминированный процесс) и носить случайный неопределенный характер (случайный процесс). Примером процесса первого рода является шум вращения воздушного винта, звук сирены; примером процесса второго рода - шум воздушной струи. Совокупность детерминированных процессов может носить характер случайного процесса (рисунок 2.3), например наложение детерминированных шумов выхлопа отдельных автомобилей дает уличный шум, имеющий случайный характер.
Периодические процессы, повторяющиеся через время Т, называемое периодом, являются детерминированными. Кратковременные процессы всегда являются непериодическими.
Случайный процесс можно представить состоящим из большого числа кратковременных непериодических процессов, отличающихся друг от друга. Случайный процесс, средние статистические характеристики которого со временем не меняются, называется стационарным, хотя он состоит из неповторяющихся элементов.
Раньше шумом называли всякий звук случайного характера. В соответствии с установившейся в настоящее время терминологией шумом будем называть всякий нежелательный звук в слышимом диапазоне частот. Поэтому при рассмотрении физических характеристик поля на практике чаще используется термин «звук », а при описании источников звука или физиологического воздействия звукового поля на человека преимущественно применяется термин «шум».
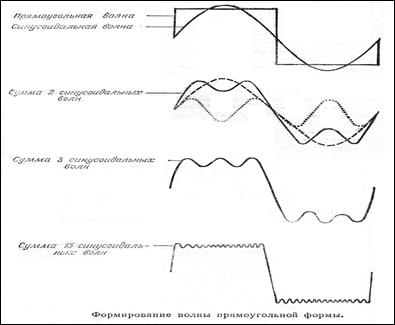
Рисунок 2.3
Спектр периодического процесса
В силу линейности уравнений акустики сложное колебание р(t) всегда можно представить в виде суммы (суперпозиции) более простых колебаний, например в виде суммы синусоидальных волн. Для периодического детерминированного процесса в какой-либо точке среды эта сумма будет иметь вид:
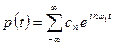 (2.24)
(2.24)
где n - целые числа, а основная круговая частота ω связана с периодом Т соотношением 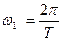 .
.
Величины С n являются комплексными амплитудами отдельных синусоидальных составляющих. Они выражаются формулой
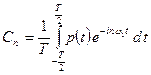 (2.25)
(2.25)
Процесс определения амплитуды Сп называется гармоническим анализом функции р(t), а величины Сп называются гармониками периодического процесса. Если учесть комплексность величины Сп, то выражение (2.24) можно представить в виде:
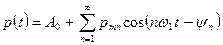
Величина А0 является постоянной слагающей; если рассматриваются отклонения физических величин в волне от невозмущенного состояния, то А0 = 0. Аргумент  называется фазой колебания, ψn - начальной фазой. Максимальное отклонение ртп называется амплитудой. Индекс п называется номером гармоники; значению п=1соответствует первая гармоника или основная частота. Колебания с кратными друг другу частотами называются гармоническими составляющими.
называется фазой колебания, ψn - начальной фазой. Максимальное отклонение ртп называется амплитудой. Индекс п называется номером гармоники; значению п=1соответствует первая гармоника или основная частота. Колебания с кратными друг другу частотами называются гармоническими составляющими.
Зависимость амплитуд ртп или фаз ψn от частоты колебаний называется соответственно спектром амплитуд или фаз. Обычно в практике борьбы с шумом интерес представляет лишь абсолютная величина (модуль) гармоник ртп безотносительно к фазе ψn.
Средний квадрат периодической функции р(t), исходя из определения средней величины, равен:
 (2.26)
(2.26)
Проделав необходимые вычисления, получим для синусоидальных составляющих
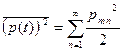 . (2.27)
. (2.27)
Это важная формула, так как она устанавливает связь мощности процесса (например, интенсивность звука в данной точке звукового поля) с амплитудами синусоидальных составляющих. Каждая величина 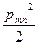 пропорциональна мощности синусоидальной составляющей с амплитудой Рmn. Таким образом, мощность периодического процесса равна сумме мощностей гармоник (энергетическое суммирование составляющих). Начальные фазы гармоник никакой роли при этом не играют.
пропорциональна мощности синусоидальной составляющей с амплитудой Рmn. Таким образом, мощность периодического процесса равна сумме мощностей гармоник (энергетическое суммирование составляющих). Начальные фазы гармоник никакой роли при этом не играют.
Зависимость 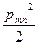 от частоты называется спектром мощности или энергетическим спектром данного процесса.
от частоты называется спектром мощности или энергетическим спектром данного процесса.
Среднее квадратическое значение физической величины 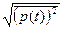 называется действующим или эффективным ее значением. Действующие значения гармоник выражаются через действующие значения амплитуд как
называется действующим или эффективным ее значением. Действующие значения гармоник выражаются через действующие значения амплитуд как 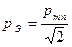 .
.
Процесс может состоять из некратных друг другу синусоидальных колебаний (почти периодический процесс, не являющийся периодическим), например сложение двух процессов с некратными друг другу периодами Т1 и Т2. В этом случае формула (2.27) также справедлива. Таким образом, средняя мощность любого детерминированного периодического или почти периодического процесса равна сумме мощностей его составляющих.
Спектр случайного процесса
Случайный процесс (каковыми в большинстве случаев являются шумы) не имеет резко выраженного периода и поэтому, в отличие от периодического процесса, не может быть выражен через гармонические составляющие. Однако он также обладает важными спектральными характеристиками.
Рассмотрим характеристику стационарного случайного шума. Установившимся во времени устойчивым процессам соответствуют обычно такие шумы, вероятностные характеристики которых не изменяются при любом сдвиге по времени. Если в бесконечной записи случайного процесса выделить несколько произвольных участков одинаковой продолжительности Т (такие участки называются реализациями данного случайного процесса) и наложить друг на друга, то записанные кривые не совпадут ни при каких Т.
Такой непрерывный процесс обладает средней мощностью и энергетическим спектром этой мощности, т. е. распределением ее по частотам колебаний. Средняя фаза в силу случайности колебания смысла не имеет.
Мощность такого процесса
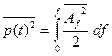 (2.28)
(2.28)
где  - средняя по времени мощность, приходящаяся на полосу частот шириной 1 гц.
- средняя по времени мощность, приходящаяся на полосу частот шириной 1 гц.
Зависимость 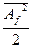 - от частоты называется энергетическим спектром данного случайного процесса или спектром его мощности. Величину
- от частоты называется энергетическим спектром данного случайного процесса или спектром его мощности. Величину 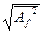 можно назвать эффективной амплитудой случайного процесса на частоте f, отнесенной к полосе шириной 1 гц.
можно назвать эффективной амплитудой случайного процесса на частоте f, отнесенной к полосе шириной 1 гц.
Вид спектра зависит от спектральных характеристик одиночных процессов, совокупность которых составляет случайный процесс, и от распределения их во времени.
Таким образом, средняя мощность периодического, почти периодического и случайного процессов равна сумме мощностей их синусоидальных составляющих.
Совсем другая .картина может наблюдаться, если складываются колебания от двух различных источников
P(t) = P1(t) + P2(t),
а не спектральные составляющие одного и того же .процесса. В этом случае:
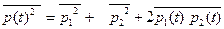 (2.29)
(2.29)
Процессы p1и р2называются некогерентными в том случае, если их взаимная мощность 2р1р2 равна нулю. Для независимых друг от друга процессов, как показывает теория вероятностей, это условие соблюдается всегда.
Степень причинной связи двух одновременных процессов характеризуется их моментом (функцией) корреляции
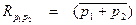 , (2.30)
, (2.30)
или нормированной величиной, называемой коэффициентом корреляции:
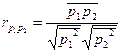 (2.31)
(2.31)
Условие равенства нулю коэффициента корреляции не всегда означает отсутствие причинной связи между составляющими, как .мы видели на примере синусоидальных составляющих одного и того же процесса.
При сложении двух процессов с одной и той же частотой они могут быть как когерентными, так и некогерентными (в зависимости от разности фаз составляющих).
Степень причинной связи во времени одного и того же случайного процесса характеризует функция автокорреляции
 (2.32)
(2.32)
где τ — время задержки. Для стационарного случайного процесса R(τ) не зависит от момента времени, принятого за нуль.
Функция автокорреляции случайного процесса однозначно связана с его спектром мощности. Функция автокорреляции и спектр мощности полностью равноправны при описании случайного процесса.
Составляющие энергетического спектра стационарного случайного процесса сами являются случайными функциями времени, и их можно считать постоянными лишь при бесконечном времени усреднения. Реальные измерительные приборы обладают конечным временем усреднения, и поэтому показания их при измерениях спектра испытывают флуктуации случайного характера, размах которых зависит от свойств прибора и ширины полосы частот. Чем эта полоса 'больше, тем флуктуации меньше.
По этой же причине при сложении случайных звуков, а также периодических сигналов, отличающихся по частоте менее чем на 10 гц, слух человека различает биения, так как время осреднения человеческого уха составляет конечную величину порядка 1 00 мсек.
Графическоео изображение спектров.
Спектр периодического .процесса с основной частотой f1 изображается , в виде зависимости амплитуд составляющих от частоты (рисунок 2.4а). На графике откладываются отрезки, пропорциональные
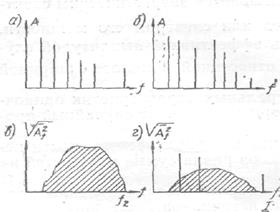
Рисунок 2.4
либо амплитудам, либо их квадратам. Начальные фазы нас не интересуют.
Спектр почти периодического процесса имеет такой же вид, только частоты не всех составляющих кратны друг другу {рисунок 2.4б). Спектры процессов, составленных из синусоид, называются дискретными или линейчатыми. Следует обратить внимание на то, что линии на таком спектре, теоретически рассуждая, не имеют ширины.
Спектр случайного или непериодического процесса (рисунок 2.4в) является оплошным, и поэтому его изображение требует обязательной оговорки о ширине ∆f элементарных полосок, к которым оно относится. По оси ординат откладываются, как показано на рисунке, либо средние квадратические значения эффективных амплитуд 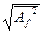 , либо соответствующие значения средних квадратов (энергий) в указанной полосе частот
, либо соответствующие значения средних квадратов (энергий) в указанной полосе частот
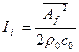 , либо действующее значение амплитуды
, либо действующее значение амплитуды  , либо уровни этих величин в дБ. Частота f1называется .нижней граничной частотой полосы спектра, а f2 — верхней. За среднюю частоту полосы обычно принимают среднюю геометрическую, равную
, либо уровни этих величин в дБ. Частота f1называется .нижней граничной частотой полосы спектра, а f2 — верхней. За среднюю частоту полосы обычно принимают среднюю геометрическую, равную
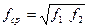 (2.33)
(2.33)
При оперировании с шумами их частотные .составляющие почти всегда считают некогерентными, и предполагают, что они подчиняются энергетическим соотношениям. Тогда, если известна эффективная амплитуда 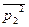 полосы ∆2 = f2-f1, то амплитуду
полосы ∆2 = f2-f1, то амплитуду 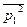 полоски ∆1f = 1 гц легко рассчитать по формуле
полоски ∆1f = 1 гц легко рассчитать по формуле
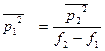 (2.34)
(2.34)
Обратный пересчет будет справедлив, если известно, что в диапазоне f2-f1 амплитуда 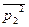 существенно не изменяется.
существенно не изменяется.
Спектр нескольких периодических и случайных процессов имеет смешанный характер (рисунок 2.4г) и изображается в виде наложения сплошного и дискретного спектров, причем совмещение их на одном графике является условным, так как амплитуда дискретной составляющей не зависит от ширины полосы спектра, а ордината сплошной части от этой ширины сильно зависит в соответствии с (2.34). Недопустимо распределять мощность дискретной составляющей по частотам в полосе, так как это не соответствует физической природе процесса.
Полосы частот.
При исследованиях шумов часто пользуются анализаторами с постоянной относительной полосой пропускания f2/f1=const. Полоса, у которой отношение f2/f1 = 2, называется октавой; если
f 2/f1 =1.26, то ширина полосы равна '/з октавы. При измерениях шумов используются также анализаторы с постоянной абсолютной полосой пропускания ∆f = const. Стандартные полосы указаны в таблице.
| Октавные полосы частот | Третьоктавные полосы частот | |||
| Граничные частоты, Гц | Среднегеометрические частоты, Гц | Граничные частоты, Гц | Среднегеометрические частоты, Гц | |
| 45-90 | 45-55 55-70 70-90 | |||
| 90-180 | 90-113 113-141 141-181 | |||
| 180-355 | 181-226 226-282 282-356 | |||
| 355-710 | 356-450 450-565 565-710 | |||
| 710-1400 | 710-900 900-1130 1130-1415 | |||
| 1400-2800 | 1415-1800 1800-2260 2260-2820 | |||
| 2800-5600 | 2820-3560 3560-4500 4500-5650 | |||
| 5600-11200 | 5650-7100 7100-9000 9000-11300 | |||
| 11200-22400 | 11300-14100 14100-18100 18100-22000 | |||
Уровень звукового давления
При анализе шума в качестве основной физической характеристики процесса обычно .выбирают уровень звукового давления. Уровень в полосе ∆f = 1 Гцназывается уровнем спектра и обозначается βШ. Исходя из условия некогерентности составляющих связь между уровнем в полосе частот f2 –f1 и уровнем спектра записывается в виде:
L(f2-f1) = 10lg 
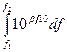 (2.35)
(2.35)
Эта формула следует из закона сложения составляющих:
 (2.36)
(2.36)
и из формулы (2.12), которую можно переписать в виде:
 (2.37)
(2.37)
Таким образом, для конечного числа составляющих суммарный уровень звукового давления равен:
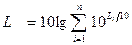 , (2.38)
, (2.38)
где n — число полос сплошного шума плюс число дискретных составляющих, или
10L/10 = 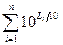 (2.39)
(2.39)
Если имеется п одинаковых составляющих с уровнем звукового давления каждой Li , то суммарный уровень звукового давления будет равен:
L = Li + 10lg n (2.40)
Чтобы облегчить вычисление суммарного уровня звукового давления при сложении “n” уровней, можно вместо формулы (2.38) воспользоваться графиком (рисунок 2.4), построенным последующему соотношению:
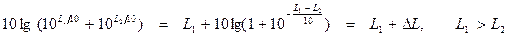 .
.
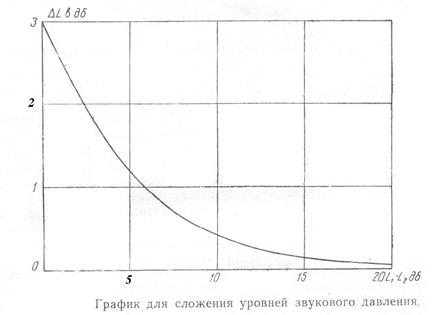
Рисунок 2.4
По оси абсцисс отсчитывается разность L1-L2 , по оси ординат - величина ∆L, которую нужно прибавить к большему уровню L1, чтобы получить суммарный уровень. Так последовательно складываются все п составляющих.
Этим же графиком удобно пользоваться при определении уровня звукового давления, развиваемого несколькими некогерентными источниками.
Пример. Определить суммарный уровень звукового давления трех компонентов, уровни каждого из которых равны L1=75 дБ, L2=62 дБ и L3=59 дБ.
Вычисляем значение L2 -L3=3 дБ; по графику находим ∆L=1,8 дБ, откуда L2”= 62+1,8=63,8 дБ; L1 – L2” =11.2 дБ; ∆L=0,3дБ; L = 75+0,3= =75,3 дБ.
Спектры, выраженные в уровнях звукового давления, обычно вычерчиваются в полулогарифмических координатах — равномерная шкала уровней и логарифмическая шкала частот.
Дата добавления: 2015-07-18; просмотров: 1772;
