Лекция 3

Излучение звука. Простейшие источники излучения – монополь, диполь, квадруполь – потенциал источника, колебательная скорость, звуковое давление, интенсивность звука и мощность источника. Ближнее и дальнее акустические поля .

Источник звука (излучатель) в безграничной атмосфере ха­рактеризуется звуковой .мощностью, частотным спектром и характеристикой направленности излу­чения.

Звуковой мощностью W называется общее количество звуко­вой энергии, излучаемой источником в единицу времени. Она оп­ределяется формулой

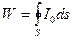(3.1)

где S — замкнутая поверхность, окружающая источник звука; I₀ — поток звуковой энергии (интенсивность) в направле­нии нормали к элементу поверхности ds. Измеряется звуковая мощность в кГм/сек или в ваттах. В .практических расчетах используется логарифмиче­ская величина - уровень звуковой мощности, аналогичный уровню звукового давления :

, (3.2)

где W₀ - постоянная величина - поток энергии с интенсивностью I₀= 10^-12 вт/(сек м²)= \0~¹³кГм/м² сек через пло­щадь 1 м², то есть:

W₀ =10^-12вт = 10^-13кГм/с (3.3)

Частотным спектром мощности излучения называется распределение излучаемой источником звуковой мощности (или уровня звуко­вой мощности) по шкале частот, то есть зависимость:

L_Wi = ψ₁ (f) (3.4)

где L_Wi - уровень звуковой мощности в i-й полосе частот; f — средняя частота этой полосы.

Обычно допустимо считать составляющие в различных полосах частот некогерентными и суммировать их мощности энергетически. Если диапазон частот звука, создаваемого источ­ником, ограничен, и спектр разбит на конечное число полос п, то для характеристики распределения звуковой мощности в спектре удобно пользоваться относительными спектрами зву­ковой мощности источника, аналогичными относительным спект­рам звукового давления, введенным в предыдущем разделе:

L_w – L_Wi = ψ₂ (f) (3.5)

где L_W - суммарный уровень звуковой мощности в заданном диапа­зоне частот.

Удобство применения относительных спектров заключается в том, что для многих процессов можно найти такую безразмерную частоту 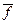, что безразмер­ный относительный спектр

L_W – L_Wi = ψ₂ ( 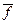) (3.6)

может характеризовать целую группу подобных источников. При конечном числе частотных полос в спектре, по аналогии с (2.39), можно записать:

10^LW/10 = 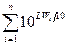(3.7)

И разделив обе части на 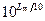, найдем соотношение нормировки для относительных спектров:

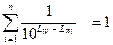(3.8)

Это соотношение может служить для контроля правильности измерения или вычисления относительных спектров.

Направленность акустического излучения источника характеризуется фактором (или коэффициентом) направленности Ф, который представляет собой отношение интенсивности звука I, создаваемого источником в данной точке, к интенсивности I_СФ, которую создал бы источник с такой же мощностью, но равномерно излучающий в среде без затухания по всем направлениям (т, е. обладающий сферической характеристикой направленности). То есть

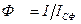(3.9)

где , r - расстояние от источника до точки наблюдения. Коэффициент направленности Ф — величина нормированная. Представив звуковую мощность в виде:

(3.10)

(где 5 — поверхность удаленной сферы, в центре которой нахо­дится источник) и .выразив из (3.9) значение I, получим

(3.11)

где 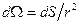- элемент телесного угла Ω, в котором распространяется звук. Это соотношение может служить для контроля правильности вычис­ления или измерения характеристики направленности.

Направленность излучения может характеризоваться также отношением интенсив­ности или звукового давления в данной точке пространства к ин­тенсивности или звуковому давлению на оси излучателя на та­ком же расстоянии от последнего.

Совокупность зависимости уровня звуковой мощности L_W,, от­носительного спектра 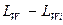, и направленности Ф_i акустического излучения от режима работы и других параметров источника называется акустической характеристикой источника.

Звуковое поле (волновая зона) сформировывается лишь на некотором расстоянии от излучателя и только там можно гово­рить о направленности излучения; в ближней зоне около излу­чателя направление движения частиц среды может не совпадать с направлением потока звуковой энергии, а зависимость между давлением и скоростью может сильно отличаться от зависимо­сти, существующей в бегущей звуковой волне.

Ближняя зона иногда называется гидродинамической, так как движение среды в ней управляется преимущественно уравнениями гидродинами­ки несжимаемой жидкости, а не акустики.

Действительно, в волновом уравнении (2.3) , выраженном через потенциал скорости, второй член пропорционален отношению потенциала к квадрату длины волны:

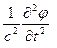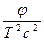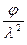~ ~ , (3.12)

где Т — характерное время процесса. Первый член уравнения пропорционален отношению потенциала к квадрату расстояния от источника до точки поля:

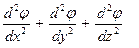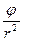~ . (3.13)

При r, меньших по сравнению с λ, можно пренебречь вторым членом, и уравнение акустики переходит в уравнение гидродина­мики несжимаемой жидкости:

. (3.14)

Таким образом, всякое решение волнового уравнения на ма­лых расстояниях от излучателя соответствует решению уравне­ний движения данного тела в несжимаемой жидкости (рассматривается неподвижная среда или движущаяся, но со скоростью, существенно меньшей скорости звука). Звуковое поле неразрывно связано с гидродинамическим полем.

Точечные источники

В акустике оперируют понятием простейших (физи­ческих) источников звука, представляющих собой неподвижные материальные точки, в которых происходят попеременное вте­кание и вытекание жидкости в окружающую среду по тому или иному закону.

Монополь - излучатель ну­левого порядка, излучающий звук равномерно по всем направлениям. Физически ему соответствует пульсирующая (расширяю­щаяся и сжимающаяся) сфера (рисунок 3.1а). Потенциал такого источника

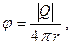(3.15)

где [Q] — количество жидкости, подаваемой источником в еди­ницу времени (расход источника) в функции аргумента (t – r/c), r - расстояние до источника

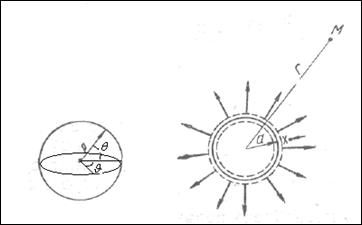
Рисунок 3.1а Прос­тейший излуча­тель звука - пульсирую­щая сфера. Слева показана характеристика направленности

При синусоидальной зависимости от времени и расстояния потенциал сферического источника пропорционален его расходу:

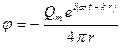(3.16)

Колебательная скорость, создаваемая таким источником в направлении г, равна:

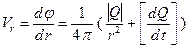(3.17)

составляющие скорости, перпендикулярные к r, для этого источ­ника .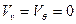

В соотношении (3.17) в квадратных скобках обозначены функции аргумента (t-r/c). Течение можно представить в виде наложения двух течений со скоростями:

,

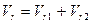, (3.18)

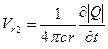
Скорость V_r1 соответствует вытеснению жидкости пульсиру­ющей сферой, так как на поверхности сферы расход .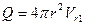

При малых “r” течение, представленное первым членом, пол­ностью соответствует течению несжимаемой жидкости. На неко­тором удалении от сферы это течение отличается от существую­щего при аналогичных условиях в полностью несжимаемой жид­кости тем, что возмущение от источника приходит в точку поля не мгновенно, а через время – r/c. Это запаздывание обусловлено сжимаемостью жидкости.

Таким образом, процесс распространения возмущения в виде звуковой волны обязательно сопровождается изменением плотности среды. Волна изменения плотности и яв­ляется звуковой волной в прямом смысле этого слова; к волно­вому полю относятся только те составляющие скорости движе­ния частиц среды, которые связаны с изменением ее плотности, а не вытеснением.

Вытеснение среды движущейся поверхностью излучателя приводит к изменению плотности у его поверхности, которое передается далее в виде звуковых волн. Поэтому источ­ником волн может быть также тело с неподвижной поверхно­стью, на которой имеются пульсации давления, приводящие к местному переменному изменению плотности. Эти пульсации мо­гут быть вызваны падающими на тело звуковыми волнами от другого источника, образованием вихрей у поверхности тела при его обтекании постоянным потоком и т. д. Звуковое давление выражается соотношением:

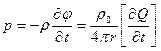, (3.19)

а изменение плотности в звуковой волне, соответствующее избы­точному звуковому давлению р, будет равно:

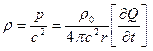, (3.20)

При большом радиусе сферы “а” волновая зона может начи­наться непосредственно на ее поверхности. В этом случае вблизи поверхности сферы на расстояниях х < a волна ведет себя как почти плоская, так как там давление слабо зависит от расстоя­ния до сферы:

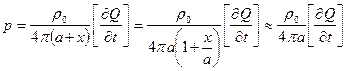(3.21)

Если потенциал зависит от времени синусоидально, то колебательная скорость и давление будут равны:

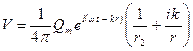(3.22)

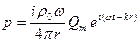(3.23)

Гидродинамическая и акустическая составляющие скорости равны друг другу при kr = 1, то есть при

.

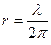Интенсивность и мощность звука, генерируемого пульсирующей сферой, выражаются соотношениями:

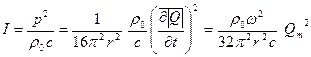, (3.24)

(3.25)

Следует обратить внимание на то, что при одном и том же расходе Q_m звуковая мощность быстро растет с увеличением ча­стоты ω. Таким образом, при сохранении неизменной амплитуды колебатель­ной скорости на поверхности излучателя его звуковая отдача (в дан­ном случае сферы) возрастает при увеличении отношения размера излучателя к длине звуковой волны. Это явление наблюдается у всех акустических излучателей.

Диполь – источник, образованный двумя простыми (сферическими) источ­никами бесконечно малых размеров с одинаковой производитель­ностью, но работающими в противофазе и находящимися па пренебрежимо малом расстоянии друг от друга (рис. 3.16). Ли­ния I, соединяющая источники, называется осью диполя. Направ­ление этой линии является условным, так как положительный источник, обозначенный значком +, через половину периода станет отрицательным, и наоборот.

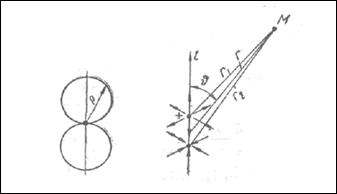
Рисунок 3.1б Прос­тейший излуча­тель звука –диполь. Слева показана характеристика направленности

Поле, создаваемое диполем, соответствует полю, создаваемо­му .поступательно колеблющейся сферой, размеры которой меньше длины звуковых волн. Сфера может быть неподвижна, а коле­бания среды относительно сферы могут вызываться посторон­ним источником (рассеивание звука на сферическом препятст­вии, колебания жидкости в вихревом следе за телом и т. д.).

Потенциал диполя равен:

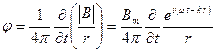. (3.26)

Выполнив дифференцирование по “t” в (3.26), получим для потенциала диполя следующее выражение:

(3.27)

где .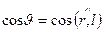

Создаваемые диполем скорости движения частиц определяются на основе соотношения (3.27):

,

(3.28)

,

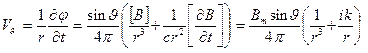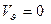. (3.29)

Давление в звуковой волне от диполя определяется выражением:

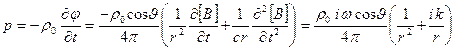. (3.30)

В случае диполя, как и для сферы, поле скорости можно представить в виде наложения совокупности скоростей ближнего .по­ля, ослабевающих с увеличением расстояния по закону , и скорости дальнего поля, ослабевающей по закону 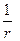. Отличие от пульсирующей сферы заключается в том, что здесь и давление можно представить в виде комбинации членов ближнего и дальнего полей.

Волновую зону излучателя можно определить как область, в которой влиянием ближних членов можно пренебречь. На рисунке 3.2 пока­заны ближнее и дальнее поля скоростей диполя для одного из моментов времени. На рисунке видно, что направление и рас­пределение скоростей в аку­стических и гидродинамиче­ских мгновенных полях могут сильно отличаться друг от друга.

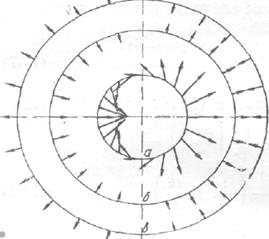
Рисунок 3.2 Ближнее (гидродинамиче­ское) и дальнее (акустическое) поля диполя в один из моментов времени а- вблизи диполя; б - вдали; в - на расстоянии А/2 от положения б (масштабы на сферах произвольны)

Чтобы вычислить звуковую мощность диполя, нужно принимать во внимание только скорости и давления в дальнем поле, так как произведения любых ближних членов, а также произведения дальних членов на ближние пропорциональны 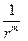, m ≥ 3, и их интеграл по сфере неогра­ниченно возрастающего ради­уса стремится к нулю, в то время как звуковая мощность не должна зависеть от радиу­са сферы, если затухания в среде не происходит. Таким образом, интенсивность звука, создаваемого диполем, направлена по радиусу и равна:

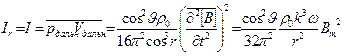. (3.31)

В силу круговой симметрии излучения относительно оси ди­поля звуковая мощность равна:

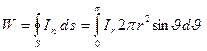(3.32)

Подставив в последнее соотношение выражение для I_r из (3.31) и выполнив интегрирование, получим:

(3.33)

Диполь можно представить в виде вектора В, направление которого совпадает с осью диполя l. Тогда физические величи­ны в дальней звуковой волне будут пропорциональны проекции этого вектора на радиус r, соединяющий рассматриваемую точку с центром диполя, а мощность можно считать состоящей из сум­мы мощностей компонентов:

,

, , ,

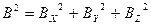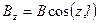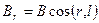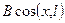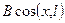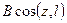= + + (3.34)

Дипольное излучение характерно для аэродинамического шума и дру­гих шумов, генерация которых обусловлена силовым воздейст­вием на среду, таких как шум лопаточных машин газотурбинного двигателя, шум воздушных винтов, шум обтекания планера воздушного судна.

Квадруполь, - источник, составленный из двух равных и противоположных по зна­ку диполей (см. рисунок 3.1в) так, что механические силы и момен­ты, действующие на квадруполь, равны нулю независимо от за­кона изменения во времени производительности “Q” каждого источника, составляющего квадруполь. Оси l₁ и l₂ диполей могут располагаться под произвольным углом друг к другу ε. Частны­ми случаями будут поперечный квадруполь, у которого оси со­ставляющих диполей расположены под .прямым углом, и про­дольный квадруполь с осями на одной прямой.

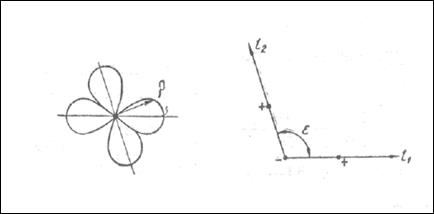
Рисунок 3.1в Прос­тейший излуча­тель звука –квадруполь. Слева показана характеристика направленности

Потенциал квадруполя

φ 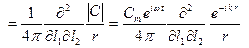(3.35)

или

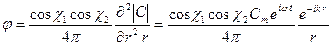(3.36)

Из последнего выражения видно, что, в отличие от диполя, квадруполь характеризуется не одним, а двумя направляющими косинусами, где С - момент квадруполя.

В дальнем звуковом поле, пренебрегая в (3.35) и (3.36) членами, убывающими как 1/rⁿ, где n ≥ 2, получим следующие выражения для колебательной скорости, звукового давления и интенсивности звука:

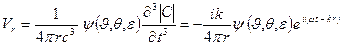(3.37)

,

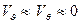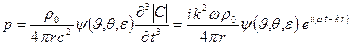, (3.38)

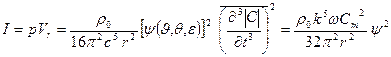, (3.39)

где ψ- функция координатных узлов и скоса диполя, которую нетрудно найти из приведенных выше формул; Ст — амплитуда момента квадруполя.

Выполнив интегрирование по сфере, получим общую фор­мулу для мощности акустического излучения квадруполя:

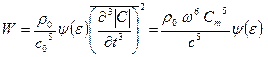, (3.40)

здесь ψ(ε)— функция конфигурации квадруполя. В гидродинамической ближней зоне квадруполя скорость убывает с расстоянием, как 1/r⁴. Квадрупольное излучение характерно для такого важного в современной технике источника шума, как турбулентная струя газа (реактивная струя ГТД).

О границе дальней волновой зоны

Каждый элемент поверхности “dS” колеблющегося тела конеч­ной величины можно считать источником сферических звуковых волн. Расход такого элементарного источника равен:

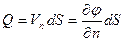, (3.41)

где n - внешняя нормаль к элементу поверхности dS; V_n - нормальная к поверхности составляющая скорости. Потенциал, создаваемый в какой-либо точке пространства М телом с произвольным распределением колебательных скоростей по поверхности, будет равен сумме потенциалов, создаваемых элементарными источниками.

Дальней (волновой) зоной .излучателя, размеры которого су­щественно меньше размеров волны, следует считать область, где уже сформировалась его характеристика направленности, и, сле­довательно, в выражениях для скорости и давления можно пре­небречь членами, обратно пропорциональными расстоянию в сте­пени выше второй включительно. Из полученных для простого источника диполя и квадруполя выражений видно, что это усло­вие соблюдается, если расстояние “r”удовлетворяет условию: .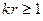

Необходимо, чтобы разность длин лучей, проведенных в точку наблюдения из центра излучателя, размеры которого существенно больше размеров .волн, и его периферии, мало отличалась от разности, которая существовала .бы для бесконечно удаленной точки, так как именно эта разность длин приводит к сформиро­ванию характеристики направленности излучателя больших раз­меров. Для точки наблюдения, расположенной на оси излучате­ля с поперечным размером “D” (рисунок 3.3), это соответствует усло­вию

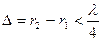. (3.42)

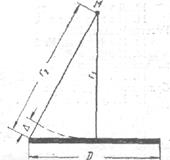
Рисунок 3.3

Поскольку 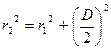и 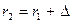, то, пренебрегая величиной ∆² по сравнению с 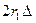, получим условие существования дальней волновой зоны:

(3.43)

Другими словами, в дальнем акустическом поле должно выполняться условие: , где а = D/2 - радиус излучателя. Для излучателя больших размеров расстоя­ние, выраженное в диаметрах излучателя, должно быть больше радиуса излучателя, выраженного в длинах волн.

Практически область волновой зоны можно найти, измеряя уровни звукового давления на различных, расстояниях от излу­чателя. До тех пор пока на лучах, соединяющих точку наблю­дения с центром излучателя, соблюдается условие:

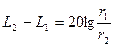(3.45)

можно считать, что практически имеет место волновая зона. Иногда оказывается, что граница волновой зоны на различных лучах соответствует разным расстояниям.