Волновое уравнение

Любое нарушение стационарности состояния упругой сплошной твердой, жидкой или газообразной среды в какой-либо точке прост­ранства приводит к появлению возмущений (волн), распростра­няющихся от этой точки.

В твердой среде могут существовать продольные волны, в которых частицы колеблются вдоль распространения вол­ны, и волны поперечные, колебания частиц в которых про­исходят в направлениях, перпендикулярных к распространению волны.

В данном разделе рассматриваются волны в газах и жидкостях, в которых могут распространяться {при отсутствии свободной по­верхности или поверхности раздела двух жидкостей) только про­дольные волны (рисунок 2.1).

Особенности звуковых волн заключаются в том, что частицы в них .колеблются относительно некоторого положения равнове­сия и скорость распространения волны (скорость звука или ско­рость, с которой перемещается максимум давления) значительно больше скорости колебания частиц (колебательной скорости) относительно положения равновесия.

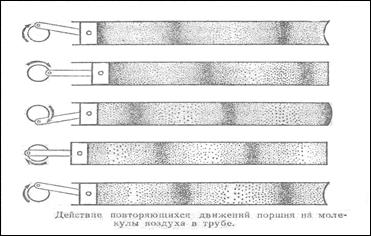
Рисунок 2.1

Рассмотрим физическую интерпретацию волнового уравнения. Для этого рассмотрим трубку с единичным поперечным сечением, наполненную средой с плотностью ρ. Выделим внутри трубки объем, ограниченный двумя плоскостями, расположенными на расстоянии dx друг от друга (рисунок 2.2). Сила, действующая на выделенный элемент в направлении оси Х, равна разности полных давлений, действующих на противоположные стороны элемента, то есть

Р₁ – Р₂ = Р(х) – Р(х + dx) ≈ - 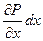(2.1)

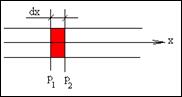
Рисунок 2.2

Если смещение левой грани элемента равно u(x), а правой u(x+dx), то относительная деформация элемента составляет 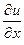. Сила инерции элемента равна 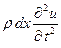. Приравнивая последнее выражение правой части (2.1), получим:

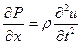- (2.2)

Продифференцируем (2.2) по координате Х и воспользуемся законом Гука (давление пропорционально степени сжатия) 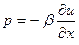, где β – сжимаемость среды (обратная величина модуля упругости 1/К). Учитывая , что 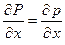, где р – мгновенное значение отклонения давления в звуковой волне от равновесного его значения Р₀, получим

; .

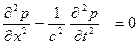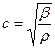Мы получили волновое уравнение для одномерного случая. Первый член волнового уравнения обусловлен сжатием элемента среды, а второй – инерцией. В трехмерном случае звуковое давление в жидкости удовлетворяет следующему волновому уравнению:

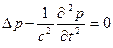, (2.3)

где 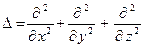- оператор Лапласа, с – скорость звука в среде. Связь между вектором колебательной скорости 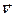и звуковым давлением в среде определяется уравнением Эйлера

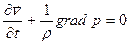, (2.4)

где .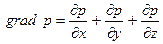

Можно считать, что градиент температуры в волне, обуслов­ленный сжатием среды, в диапазоне частот звуковых волн, встре­чающихся в практике борьбы с шумом, так мал, что явления теплообмена между соседними частицами не имеют места, и ко­лебательный процесс является адиабатическим. Тогда скорость звука

,

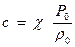где χ = Ср/С_V - показатель адиабаты (для воздуха χ = 1,41); Ср —теплоемкость воздуха при постоянном давлении; С_V - теплоемкость при постоянном объеме; ρ₀ - плотность (масса единицы объема) покоящейся среды.

Изменение давления и изменение плотности, отсчитанные от равновесных значений Р₀ и ρ₀, в звуковой волне связаны соотно­шением .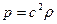

Звуковое поле является векторным полем, поскольку движение каждой частицы описывается вектором колебательной скорости 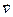с компонентами v_x, v_y, v_z. В идеальной жидкости при отсутствии вязкости равнодействующая сил, действующих на элемент среды, проходит через его центр и вращательный момент равен 0, то есть выполняется условие 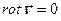. В этом случае звуковое поле является незавихренным и его можно охарактеризовать исчерпывающим образом одной скалярной функцией - потенциалом скорости φ (х, y, z, t). По известному потенциалу скорости можно определить звуковое давление и колебательную скорость. Колебательная скорость равна

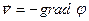, (2.5)

а, воспользовавшись уравнением Эйлера (2.4), получим:

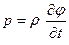. (2.6)

Наряду с волновым уравнением (2.3) в акустике для описания волновых процессов широко используется уравнение Гельмгольца, которое получается при подстановке в уравнение (2.3) звукового давления в комплексном ви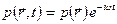де , где 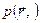- амплитуда колебания, ω – угловая частота:

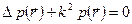(2.7)

В уравнении Гельмгольца (2.7) физический смысл имеет лишь вещественная часть давления.

В математической физике волновое уравнение относится к уравнениям гиперболического типа (члены уравнения имеют разные знаки), а уравнение Гельмгольца – к уравнениям эллиптического типа (все члены уравнения имеют одинаковый знак). Методы решения этих уравнений существенно различаются.

Физическое различие между гиперболическими и эллиптическими уравнениями хорошо иллюстрируется на примере акустики движущейся среды. Уравнение Блохинцева, описывающее распространение звука в среде, движущейся в направлении оси Х со скоростью u=Mc, где М – число Маха, имеет вид:

.

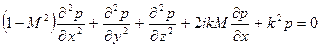Если М<1, то уравнение является эллиптическим и звуковые поля в среде, движущейся с дозвуковой скоростью, не отличаются качественно от полей в неподвижной среде. Если же M>1, то уравнение становится гиперболическим. Решения таких уравнений рассматриваются в газодинамике больших скоростей, когда в поле течения появляются скачки уплотнения и ударные волны, в частности, при исследовании распространения звукового удара от сверхзвукового самолета.