IX.2. Колебательные контуры и их параметры.

Существует два типа одиночного колебательного контура: последовательный и параллельный. В последовательном колебательном контуре, изображённом на рис.9.2, индуктивность L_К, ёмкость C_К, и активное сопротивление R_К соединены последовательно с источником напряжения U_ИСТ.

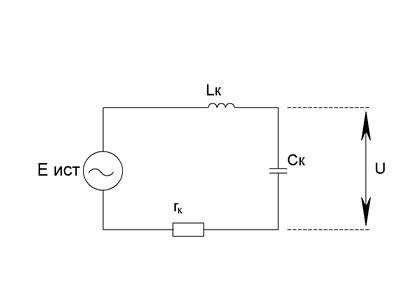
Рис.9.2. Схема последовательного колебательного контура.

Ток в этом колебательном контуре равен

I = U_ИСТ./ ÖR²_К + (wL_К – 1/ wС_К)² ………………. (9.1).

На резонансной частоте w = w₀ реактивное сопротивление контура становится равным нулю, т.е. выполняется условие

w₀L_К = 1/ w₀С_К …………………………………… (9.2).

Отсюда резонансная частота контура определяется формулой Томсона:

w₀ = 1/ Ö L_KC_K и f₀ = 1/ 2pÖ L_KC_K ……………… (9.3).

При этом ток в контуре достигает максимального значения

I_m = U_ИСТ / R_K ……………………………. (9.4).

В момент резонанса реактивные сопротивления индуктивности и ёмкости во много раз больше активного сопротивления контура:

Х_L = wL_К >> R_К и X_C = 1/ wC_К >> R_К …….. (9.5),

откуда следует, что напряжения на реактивных элементах контура при резонансе во много раз больше приложенного напряжения источника сигнала:

U_L >> U_ИСТ. и U_C >> U_ИСТ. ………………… (9.6).

Отсюда и происходит термин резонанс напряжений, или последовательный резонанс.

Реактивное сопротивление индуктивности Х_L и реактивное сопротивление ёмкости Х_C в момент резонанса называется волновым (характеристическим) сопротивлением резонансного контура (r):

r = w₀L_К = 1/ w₀C_К = Ö L_К / C_К ………………. (9.7).

В колебательных контурах всегда r>> R_К.

Отношение напряжения на одном из реактивных элементов (индуктивности или ёмкости) к напряжению источника назовём коэффициентом передачи напряжения контура:

К_U = U_C / U_ИСТ.= U_L / U_ИСТ. ……………………… (9.8)

В момент резонанса, когда частота источника точно равна резонансной частоте контура, ток в контуре достигает максимальной величины, а значит, и напряжение на реактивных сопротивлениях достигает максимального значения. При этом коэффициент передачи напряжения также достигает максимального значения, называемого добротностью контура (Q):

К_U = K_{U max}.= Q = U_L / U_ИСТ. = U_C / U_ИСТ. …………………… (9.9).

После несложных преобразований получим:

Q = w₀L_К/ R_К = 1/ w₀С_КR_К = r / R_К ……………… (9.10).

Добротность резонансных контуров с сосредоточенными параметрами в диапазоне 100 кГц ¸ 1 МГц может достигать до 300 в зависимости от частоты и качества их исполнения. Добротность резонансных контуров с распределёнными параметрами (волноводы, резонаторы и др.) может достигать нескольких тысяч и даже десятков тысяч.

Величина, обратная добротности, называется затуханием контура (d):

d = 1/ Q = R_К / r ……………………………… (9.11).

При изменении частоты источника напряжения в ту или иную сторону от резонансной частоты ток в контуре уменьшается и, соответственно, уменьшается коэффициент передачи напряжения контура.

Отношение добротности контура к коэффициенту передачи напряжения при заданной расстройке Df называется избирательностью резонансного контура и обозначается через Se:

Se = Q / K_U ……………………………… (9.12).

Если в выражения (9.8) и (9.12) подставить параметры контура и произвести некоторые преобразования, то получим зависимость избирательности от величины расстройки Df:

Se = (w / w₀)×Ö 1 + Q² ×[(w / w₀) – (w₀ / w)] ² …………… (9.13).

При относительно малых расстройках (не более 10 %), что имеет место в одиночных резонансных контурах, можно считать:

w + w₀ » 2w и w / w₀ »1 ……………… (9.14).

Тогда, преобразовав сомножитель под корнем (9.13), получим:

(w / w₀) – (w₀ / w) » 2w×Dw / w₀ × w = 2Dw / w₀ ……. (9.15).

Отсюда

Se = Ö1 + Q² ×(2Dw / w₀)² = Ö1 + Q² ×(2Df / f₀)² ………. (9.16),

где Df = ½f – f ₀½.

Величина 2Df / f₀ называется удвоенной относительной расстройкой, а величина

Q·2Df / f₀ = d ………………………………………. (9.17) называется обобщённой расстройкой контура. Обобщённая расстройка учитывает все основные параметры контура: расстройку Df , резонансную частоту f₀ и добротность Q.

Окончательно получим:

Se = Ö(1 + d²) ……………………………. (9.18).

Это уравнение определяет форму кривой избирательности одиночного резонансного контура.

На рис.9.3 по этому выражению построена кривая.

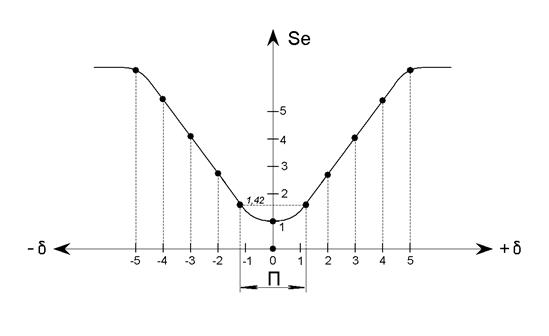
Рис. 9.3. Зависимость избирательности контура от обобщённой расстройки.

Строго говоря, кривая, построенная по уравнению (9.18), несимметрична относительно резонанса. Однако в большинстве случаев кривая избирательности интересна для случаев небольших (не более 10 %) отклонений от резонансной частоты. В этом случае можно без большой погрешности считать кривую избирательности симметричной относительно резонансной частоты. Для больших расстроек кривая избирательности строится по выражению (9.13), и она получается несимметричной.

Иногда кривую избирательности строят по выражению

Y = 1 / Se …………………………. (9.19).

В этом случае она имеет вид, изображённый на рис.9.4.

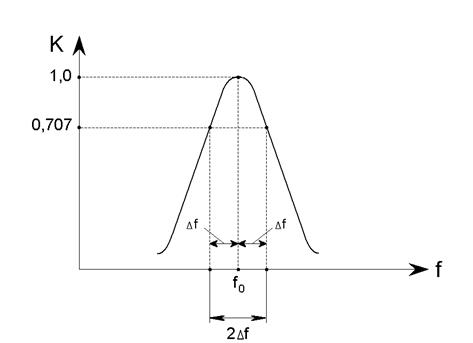
Рис. 9.4. Резонансная кривая колебательного контура.

Выражение (9.19) и кривая (рис.9.4), построенная по этому выражению, является амплитудно-частотной характеристикой одиночного резонансного контура, называемой резонансной кривой.

Из этого рисунка видно, что даже при небольшой расстройке контура происходит уменьшение усиления. При действии на контур модулированной ЭДС принципиально неизбежны искажения формы сигнала, обусловленные неравномерностью резонансной характеристики контура, так как часто¢ты различных составляющих спектра ЭДС отличаются от резонансной частоты контура. Для ослабления искажений необходимо так выбирать параметры контура, чтобы в полосе частот, содержащей основную часть энергии модулированного колебания, усиление составляющих спектра подводимой ЭДС было по возможности равномерным. Эта полоса частот называется полосой пропускания контура.

В радиотехнике принято следующее определение полосы пропускания колебательного контура:

Полоса пропускания колебательного контура – это полоса частот вблизи резонанса, на границах которой амплитуда тока (или напряжения) уменьшается в Ö 2 раз от резонансного значения. При этом амплитуда действующей на контур ЭДС считается неизменной.

Иначе говоря, в пределах полосы пропускания (П) уменьшение усиления происходит не более чем в Ö2 раз по сравнению с максимальным усилением, что соответствует уменьшению мощности сигнала в два раза. Таким образом, ширина полосы пропускания отсчитывается по уровню 0,707 от максимума резонансной кривой. Эту величину можно получить, приравняв

d = Q × 2Df / f₀ = ± 1. Тогда из выражения (9.18) следует Se = Ö2 и

1/Se = 0,707.

Из рис.9.3 и 9.4 видно, что полоса пропускания П = 2Df . Следовательно,

d = Q×П /f₀ и окончательно получаем:

П = f₀ / Q ……………………. …. (9.20).

Отсюда можно сделать вывод, что полоса пропускания одиночного колебательного контура непосредственно определяется его добротностью.

При увеличении добротности контура уменьшается его полоса пропускания и наоборот.

В параллельном контуре наблюдается резонанс токов, т.е. в момент резонанса ток в контуре I_К >> I_ИСТ. При этом сопротивление параллельного контура достигает максимального значения, называемого резонансным сопротивлением R_РЕЗ, определяемого по формуле

R_РЕЗ. = L_К / R_К×C_К ……………………….. (9.21).

Резонансное сопротивление имеет не только максимальное, но и чисто активное значение. При расстройке контура в ту или другую сторону эквивалентное сопротивление параллельного контура не только падает, но и приобретает индуктивный или емкостный характер.

Добротность параллельного контура Q показывает, во сколько раз ток в одной из ветвей контура в момент резонанса больше тока источника ЭДС.

В общем случае формулы, выведенные для последовательного контура, не пригодны для параллельного контура. Однако если считать, что внутреннее сопротивление источника ЭДС (R_i) значительно больше резонансного сопротивления контура R_i >> R_РЕЗ. (что практически всегда имеет место в резонансных усилителях), то характер изменения напряжения на контуре при изменении частоты источника ЭДС будет таким же, как и в последовательном контуре, а поэтому формулы останутся прежними. Это можно подтвердить и математически, приведя параллельный резонансный контур к эквивалентной схеме последовательного.