Колебательные звенья. Особые звенья: неминимально-фазовые устойчивые звенья, неустойчивые звенья

Колебательное звено описывается уравнением второго по­рядка

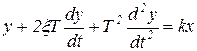(1.7.48)

при степени затухания 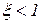, что соответствует комплексным корням характеристического уравнения

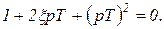
Постоянная времени Т колебательного звена связана с его резонансной частотой ω₀ соотношением

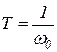(1.7.49)

и в 2π раз меньше периода резонансных колебаний

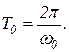(1.7.50)

Примерами колебательного звена могут служить упругая механическая система с существенным влиянием массы, электрический колебательный контур (рисунок 1.7.14).

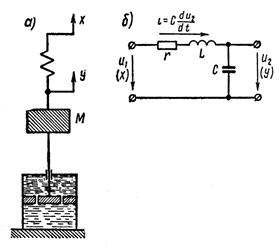
Рисунок 1.7.14 – Примеры колебательного звена

Комплексный коэффициент усиления колебательного звена

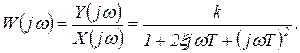(1.7.51)

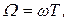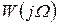Вводя безразмерную частоту можно выразить следующим образом:

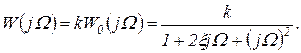(1.7.52)

На рисунке 1.7.15, а, б, в показаны частотные характеристики колебательного звена. Как видно из рисунка 1.7.15, а, годограф частотной характеристики проходит через два квадранта IV и III и пересекает мнимую ось при 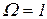. При этом

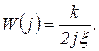
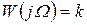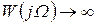С уменьшением ξ петля, охватываемая годографом, увеличи­вается (см. пунктир), и при характеристика вырождается в две полупрямые: I — от до при 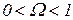и II ― от 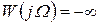до при 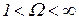. Инверсная характеристика 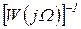проходит через два квадранта I и II и уходит в бесконечность параллельно веще­ственной оси при .

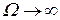Амплитудно-частотная и фазочастотная характеристики выражаются урав­не­ниями:

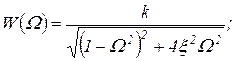(1.7.53)

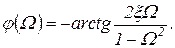(1.7.54)

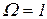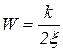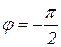При эти характеристики соответственно проходит через точки и . При 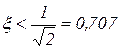кривая 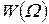имеет максимум

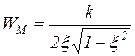(1.7.55)

при

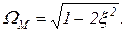(1.7.56)

Передаточная функция колебательного звена

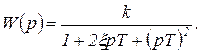(1.7.57)

Корнями характеристического уравнения 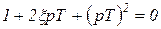будут

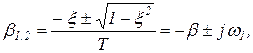
где 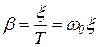— коэффициент затухания;

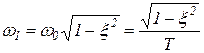― собственная частота колебаний звена.

Переходная функция

(1.7.58)

Весовая функция

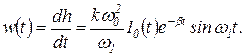(1.7.59)

Графики переходной и весовой функций колебательного звена показаны на рисунке 1.7.15, г и д.

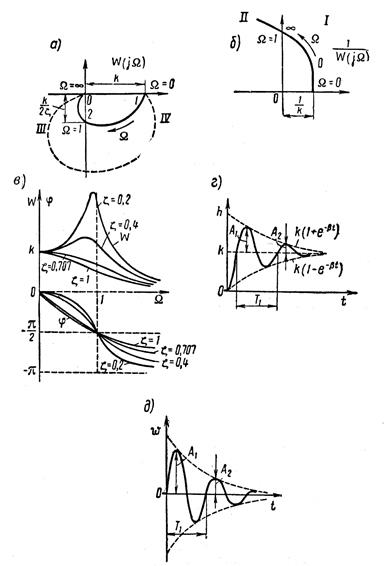
Рисунок 1.7.15 – Характеристики колебательного звена

Кроме рассмотренных типовых линейных звеньев, в системах автоматического управления встречаются звенья, которые по характеристикам существенно отличаются от типовых. К числу таковых относятся: неминимально-фазовые звенья, передаточные функции которых дробно-рациональны и имеют нули в правой полуплоскости: неустойчивые звенья, имеющие полюса в правой полуплоскости; звенья с распредел­ёнными параметрами, которые могут быть разделены на ир­рациональные звенья, описываемые иррациональными переда­точными функциями, и трансцендентные, описываемые транс­цендентными передаточными функциями. В звеньях с распреде­ленными параметрами количество особенностей передаточных функций может стремиться к бесконечности и анализ динамиче­ских свойств системы требует рассмотрения вспомогательных вопросов. Это связано с тем, что звено описывается уже не обыкновенными линейными дифференциальными уравнениями, а уравнениями в частных производных.

Рассмотрим звенья каждой из всех перечисленных групп и примеры реальных элементов, соответствующих им.