Неустойчивые звенья

Наиболее общая форма уравнения неустойчивого звена пер­вого порядка может быть записана как

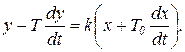(1.7.69)

Передаточная функция

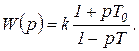(1.7.70)

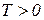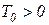Уравнения (1.7.69) и (1.7.70) отличаются от (1.7.40) и (1.7.42) только знаком при Т. Все виды звеньев первого порядка мож­но описать одним и тем же уравнением (1.7.40), если считать, что при и звено — минимально-фазовое типовое; пр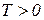и и звено — неминимально-фазовое устойчи­вое; при 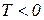вне зависимости от знака 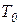звено — неустой­чивое.

На рисунке 1.7.19 показаны примеры расположения нулей и полюсов передаточ­ных функций звеньев первого порядка при различных знаках Т и 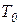в уравнении (1.7.40).

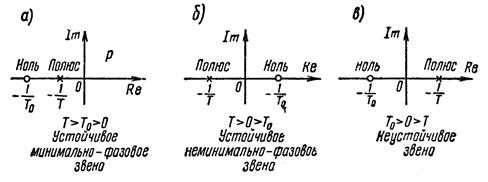
Рисунок 1.7.19 – Расположение нулей и полюсов передаточной функции на комплексной плоскости

Наиболее распространенным примером неустойчивого звена является квазиинерционное звено, для которого 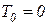. В этом случае, в зависимости от выбора положительных направлений х и у получаем

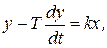(1.7.71)

или

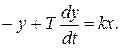(1.7.72)

Комплексный коэффициент усиления неустойчивого квази­инерционного звена

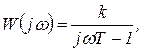(1.7.73)

а передаточная функция

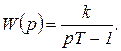(1.7.74)

Годографы амплитудно-фазовой характеристики неустойчи­вого квазиинерционного звена показаны на рисунке 1.7.20, а и б. Как видно из построения, прямой и инверсный годографы комплек­сного коэффициента усиления представляют собой зеркальные отображения относительно мнимой оси годографов, полученных для инерционного звена (см. рисунок 1.7.8).

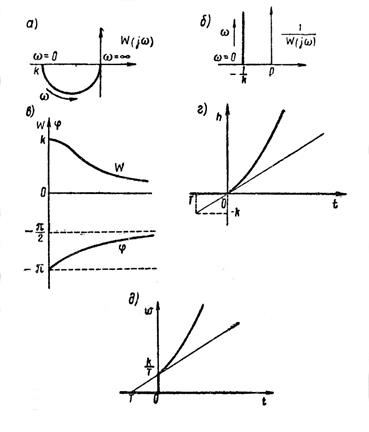
Рисунок 1.7.20 – Характеристики неустойчивого звена

Амплитудно-частотная характеристика имеет то же выра­жение, что и для типового инерционного звена

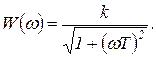(1.7.75)

Таким образом, график 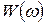рассматриваемого неустойчивого звена ничем не отличаются от аналогичного гра­фика типового инерционного звена. Фазочастотная характеристика

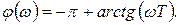(1.7.76)

Эта зависимость (рисунок 1.7.20, в) представляет собой зеркальное отображение фазочастотной характеристики инерционного звена относительно прямой 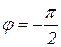, соответствующей мнимой оси.

Из рассмотрения полученных частотных характеристик можно сделать вывод, что неустойчивые звенья могут иметь точно такие же амплитудно-частотные характери­стики, как и устойчивые звенья, однако при этом фазочастотные характеристики существенно различаются.

По передаточной функции (1.7.74) может быть найдена пере­ходная функция (рисунок 1.7.20, г)

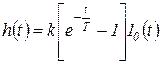(1.7.77)

и весовая функция (рисунок 1.7.20, д)

(1.7.78)

Для линейных неустойчивых звеньев не существует устано­вившегося режима, и с течением времени при любой входной величине выходная величина стремится в бесконечность.