Звенья первого порядка

Инерционное звено. Одним из самых распространен­ных звеньев системы автоматического управления является инерционное звено. Оно описывается уравнением

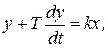(1.7.19)

где k и Т — соответственно коэффициент усиления и постоян­ная времени звена.

Примерами инерционного звена (рисунок 1.7.7) могут служить RC- и RL-цепочки.

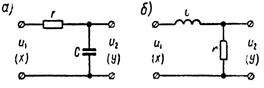
Рисунок 1.7.7 – Примеры инерционного звена

Комплексный коэффициент усиления

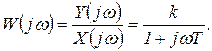(1.7.20)

Частотные характеристики для этой функции показаны на рисунке 1.7.8, а, б. Здесь

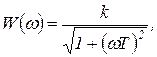(1.7.21)

а

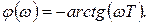(1.7.22)

Наряду с характеристикой 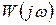иногда бывает удобно поль­зоваться инверсной характеристикой 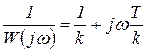. Для инерционного звена такая характеристика показана на рисунке 1.7.8, б. Если характеристика 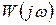имеет вид типичной круговой диаграммы, лежащей в четвертом квадранте и опирающейся на диаметр 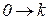, то инверсная характеристика имеет вид прямой, уходящей из точки 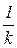в бесконечность параллельно мнимой оси.

Передаточная функция инерционного звена согласно (1.7.20)

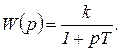(1.7.23)

Соответственно переходная функция

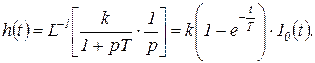(1.7.24)

Весовая функция

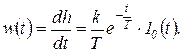(1.7.25)

Графики переходной и весовой функций инерционного звена показаны на рисунке 1.7.8, г и д.

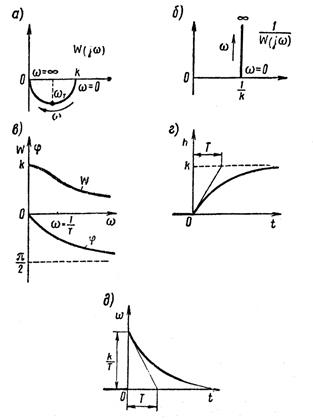
Рисунок 1.7.8 – Характеристики инерционного звена

Форсирующее звено. Звено, описываемое дифферен­циальным уравнением

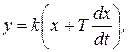(1.7.26)

называется форсирующим звеном.

Такое звено получается в результате различных параллель­ных соединений пропорционального и дифференцирующего или инерционного звеньев.

Для этого звена получаем:

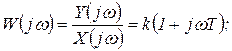(1.7.27)

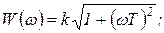(1.7.28)

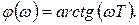(1.7.29)

Частотные характеристики форсирующего звена показаны на рисунке 1.7.9. Как видно из графика, прямая амплитудно-фазо­вая характеристика форсирующего звена аналогична инверсной характеристике инерционного звена, а инверсная его характе­ристика соответствует прямой характеристике инерционного звена.

Это соответственно отражается и на амплитудных и фазо­вых характеристиках.

Передаточная функция форсирующего звена

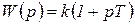(1.7.30)

и может быть представлена в виде суммы передаточных функ­ций пропорционального и дифференцирующего звеньев. Переходная и весовая функции форсирующего звена имеют вид суммы соответствующих функций простейших звеньев:

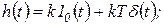(1.7.31)

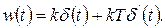(1.7.32)

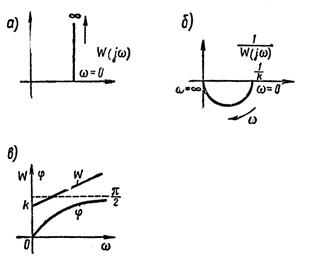
Рисунок 1.7.9 – Характеристики форсирующего звена

Инерционно-дифференцирующее звено. Звено, описываемое дифференциальным уравнением

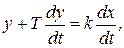(1.7.33)

называется реальным дифференцирующим, или инерционно-дифферен­циру­ющим звеном.

Примерами такого звена являются механическая система с гибкой гидравлической связью и четырехполюсники, содер­жащие соответствующим образом включенные активные и реак­тивные сопротивления (рисунок 1.7.10).

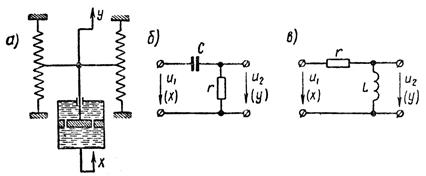
Рисунок 1.7.10 – Примеры инерционно-дифференцирующего звена

Комплексный коэффициент усиления

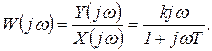(1.7.34)

Частотные характеристики для этой функции показаны на рисунке 1.7.11, а, б, в:

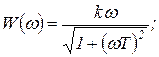(1.7.35)

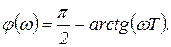(1.7.36)

Передаточная функция инерционно-дифференцирующего звена согласно (1.7.34)

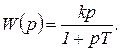(1.7.37)

Переходная функция:

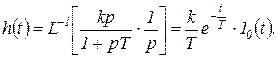(1.7.38)

Весовая функция:

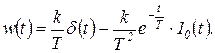(1.7.39)

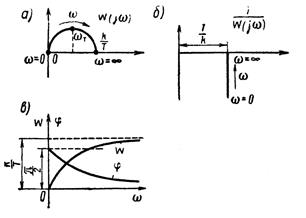
Рисунок 1.7.11 – Характеристики инерционно-дифференцирующего звена

Инерционно-форсирующее звено. Инерционно-фор­сирующим (или упругим) называется звено, описываемое диф­ференциальным уравнением следующего вида

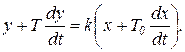(1.7.40)

Существенным параметром инерционно-форсирующего звена является коэффициент 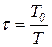. Если 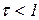, то звено по своим свойствам приближается к интегрирующему и инерци­онному звеньям. Если же 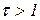, то звено — ближе к дифференцирующему и инер­ционно-дифференцирующему звеньям.

Комплексный коэффици­ент усиления инерционно-форсирующего звена

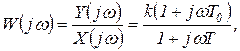(1.7.41)

а передаточная функция

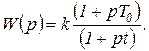(1.7.42)

На рисунке 1.7.12 построены частотные характеристики при 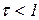(а, в, д)и 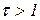(б, г, е). Характеристики построены для нормированных значений

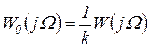
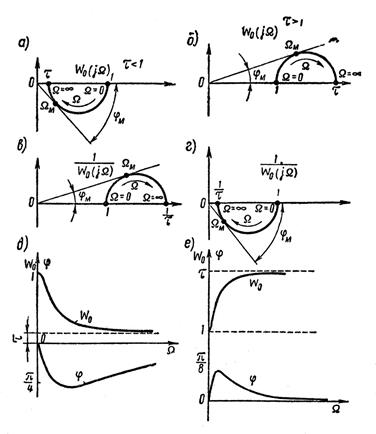
Рисунок 1.7.12 – Характеристики инерционно-форсирующего звена

в зависимости от относительной безразмерной частоты 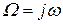. Здесь

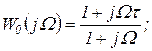(1.7.43)

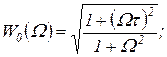(1.7.44)

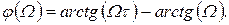(1.7.45)

Переходная функция определяется как

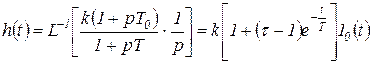(1.7.46)

и, соответственно,

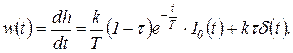(1.7.47)

Переходные и весовые функции для инерционно-форсирую­щих звеньев показаны на рисунке 1.7.13 (при 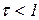(а и в); при 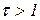(б и г)).

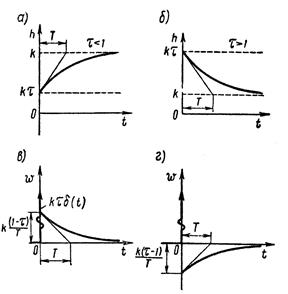
Рисунок 1.7.13 – Переходная и весовая функция
инерционно-форсирующего звена