Простейшие звенья

Пропорциональное звено. Самым простым является звено, выходная величина которого прямо пропорциональна входной величине. Уравнение такого звена

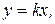(1.7.1)

где k — коэффициент усиления звена.

Примерами такого звена (рисунок 1.7.1) являются: делитель на­пряжения (а), усилитель постоянного тока (б),рычажная пере­дача (в), редукторная передача (г) и др.

Предполагается, что передача сигнала от входа к выходу про­изводится мгновенно без какой-либо инерции. Поэтому, пропор­циональные звенья называются безынерционными.

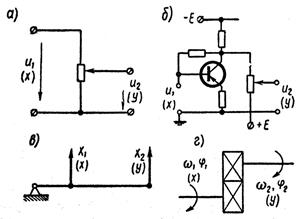
Рисунок 1.7.1 – Примеры пропорционального звена

Если на вход пропорционального звена подать синусоидаль­ный сигнал

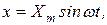
то на выходе появится сигнал

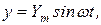
где

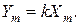
В комплексной форме

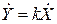
или

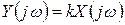(1.7.2)

и комплексный коэффициент усиления

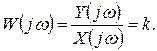(1.7.3)

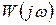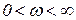Годограф комплексного коэффициента усиления при имеет вид точки, сдвинутой на расстояние k от нуля по вещественной оси (рисунок 1.7.2, а).

Принятое описание связи между входом и выходом соответ­ствует идеальному звену, а для реального звена справедливо только при частотах, меньших определенной максимальной ве­личины .

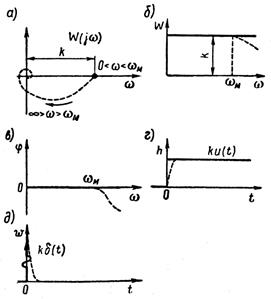
Рисунок 1.7.2 – Характеристики пропорционального звена

При возрастании ω до бес­конечности коэффициент усиления любого реального звена снижается до нуля и годограф коэффициента усиления при 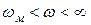носит характер графика, пока­занного на рисунке 1.7.2, а пунктиром. Однако в системах автомати­ческого управления обычно рассматривается диапазон сравни­тельно низких частот, для которых 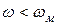и, все рассмотренные устройства могут быть отнесены к категории пропорциональных (безынерционных) звеньев, а годограф коэффициента усиления имеет вид точки k.

Соответствующие амплитудно-частотные и фазочастотные характеристики показаны на рис. 1.7.2, б и в.

Переходя от коэффициента усиления к передаточной функции

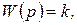(1.7.4)

а затем к переходной и весовой функциям, получаем

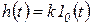(1.7.5)

и

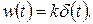(1.7.6)

Графическое изображение переходной и весовой функций пропорционального звена показано на рисунке 1.7.2, г и д. Обе эти функции соответствуют идеальному пропорциональному звену. Реальные звенья, схемы которых изображены на рисунке 1.7.1, имеют характеристики, только приближенно описываемые этими гра­фиками. Отклонение реальных характеристик от идеальных на графиках показано пунктиром (см. рисунок 1.7.2).

Интегрирующее звено. Существует ряд звеньев, в ко­торых выходная величина пропорциональна или равна интегралу по времени от входной величины

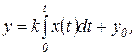(1.7.7)

где k — некоторый коэффициент пропорциональности.

Такие звенья называются интегрирующими.

Примерами реальных элементов, эквивалентные схемы которых сводятся к интегрирующему звену, являются: электрическая емкость (рисунок 1.7.3, д), индуктивность (б), вращающийся вал (в), гидравличе­ский резервуар (г).

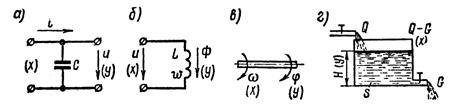
Рисунок 1.7.3 – Примеры интегрирующего звена

Если на вход интегрирующего звена подать синусоидальный сигнал 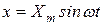, то из уравнения (1.7.7) непосредственно следует, что

(1.7.8)

или

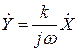
и

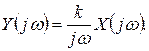(1.7.9)

Комплексный коэффициент усиления интегрирующего звена

(1.7.10)

Частотный годограф (а) и частотные характеристики (б)интегрирующего звена показаны на рисунке 1.7.4.

Переходя от коэффициента усиления к передаточной функции

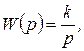(1.7.11)

а затем к переходной и весовой функциям, получаем

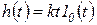(1.7.12)

и

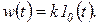(1.7.13)

Переходная и весовая функция интегрирующего звена представлены на рисунке 1.7.4, в и г.

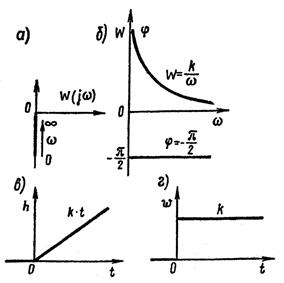
Рисунок 1.7.4 – Характеристики интегрирующего звена

Дифференцирующее звено. Не существует такого реального элемента, в котором на выходе точно воспроизво­дилась бы производная от любого входного сигнала. Однако при составлении структурной схемы системы ее можно так разделить на звенья, что введение понятия дифференцирую­щего звена будет вполне обосновано.

В этом случае выходная величина у зависит от входной величины х как производная

(1.7.14)

где k — коэффициент пропорциональности.

Примерами таких звеньев могут служить электрическая ёмкость, индуктивность (рисунок 1.7.5).

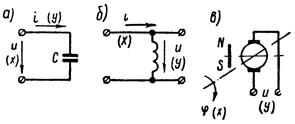
Рисунок 1.7.5 – Примеры дифференцирующего звена

Комплексный коэффициент усиления

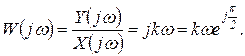(1.7.15)

Все частотные характеристики звена представлены на рисунке 1.7.6, а, б.

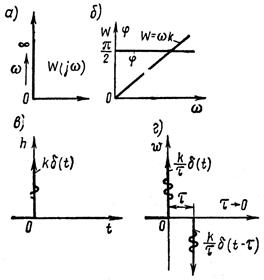
Рисунок 1.7.6 – Характеристики дифференцирующего звена

Передаточная функция дифференцирующего звена

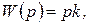(1.7.16)

а, соответственно, переходная и весовая функции

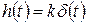(1.7.17)

и

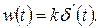(1.7.18)

Переходная и весовая функция дифференцирующего звена представлены на рисунке 1.7.6, в и г. Производная от δ-функции или δ-функция второго порядка δ' на рисунке 1.7.6, г изображена в виде двух импульсов второго порядка, интервал между которыми τ стре­мится к нулю.