Устойчивость линейных звеньев. Минимально-фазовые звенья. Преобразование произвольного сигнала линейным звеном

Из рассмотрения выраже­ния (1.5.15) можно сделать вывод о зависимости устойчивости системы от того, в какой области лежат корни .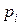

Для линейных систем определение устойчивости объекта или звена может быть сформулировано более жестко, чем для общего случая.

Линейное звено является устойчивым, если после окон­чания внешнего воздействия оно с течением времени возвратится к исходному состоянию.

Единичный импульс может быть рассмотрен как кратковре­менное воздействие. В таком случае о линейном звене можно судить по значению при : звено устойчиво, если

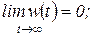(1.6.1)

звено неустойчиво, если

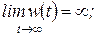(1.6.2)

звено нейтрально, если

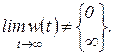(1.6.3)

Каждому действительному значению 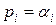соответствует в выражении (1.5.15) слагаемое вида

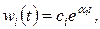(1.6.4)

где

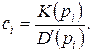(1.6.5)

Комплексной паре корней характеристического уравнения

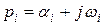
и

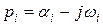
соответствует слагаемое вида

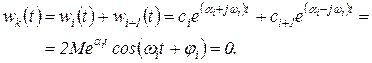(1.6.6)

Следует различать три случая расположения корней:

1) вещественная часть корня положительна ( ),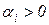

2) вещественная часть корня отрицательна ( ),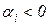

3) вещественная часть корня равна нулю ( ).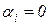

В первом случае корень лежит в правой полуплоскости корней, т.е. правее мнимой оси, во втором случае — в левой полуплоскости, т.е. левее мнимой оси (рисунок 1.6.1). В третьем случае он лежит на мнимой оси.

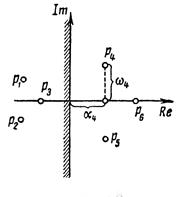
Рисунок 1.6.1 – Расположение корней относительной мнимой оси

В зависимости от расположения кор­ней относительно мнимой оси характер изменения составляющих 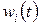во вре­мени различен. При 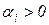(рисунок 1.6.2, а) соответствующая составляющая при 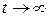стремится к бесконечности, и, сле­довательно, к бесконечности стремится и вся величина 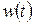— звено неустойчиво.

При 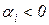(рисунок 1.6.2, б) соответствующая составляющая при 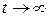стремится к нулю и, следовательно, если все составляющие, число которых конечно, удовлетворяют этому условию, то 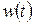также стремится к нулю — звено устойчиво.

При (рисунок 1.6.2, в) при 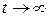составляющая остается конечной и не равна нулю — звено нейтрально.

На рисунке 1.6.2 для каждого случая расположения корней пока­заны графики при действительном корне (наверху) и при паре сопряженных комплексных корней (внизу).

Таким образом, необходимым и достаточным условием устойчивости линейного звена является отрицательное значение вещественной части всех полюсов функции 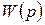, т.е. все полюсы должны лежать в левой полуплоскости p.

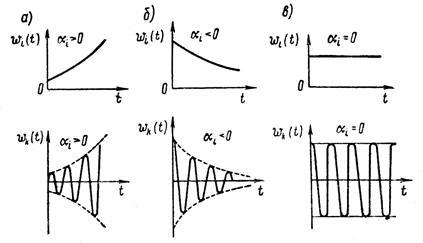
Рисунок 1.6.2 – Поведение составляющих 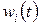при различных значениях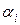

Важным общим показателем свойств звена является принад­лежность нулей передаточной функции к левой полуплоско­сти р. Рассматривая передаточную функцию, записанную в фор­ме (1.15), можно комплексный коэффициент усиления выразить как

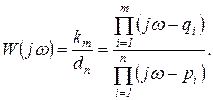(1.6.7)

Рассмотрим один сомножитель числителя 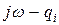. Эта раз­ность представляет собой вектор, начало которого лежит в точке 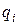, а конец — на мнимой оси в точке 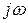. Фаза этого вектора вы­ражает поворот его относительно вещественной оси против часовой стрелки.

На рисунке 1.6.3 построены два та­ких вектора для различных поло­жений точки 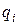, обозначенных 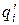и 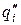. Из построения видно, что при одном и том же значении мо­дуля комплекса 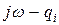его фаза φ меньше в том случае, ког­да 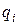лежит в левой полуплоскости. Поэтому звенья, все нули передаточных функций которых лежат в левой полуплоскости ( 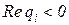), называются минимально-фазовыми.

Звенья, передаточные функции которых имеют хотя бы один нуль, лежащий в правой полуплоскости ( 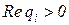), называются неминимально-фазовыми.

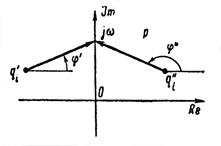
Рисунок 1.6.3 – Расположение вектора 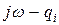относительно мнимой оси

Для минимально-фазовых устойчивых звеньев между амплитудно-частотной и фазочастотной характеристиками существует однозначная зависимость и, следовательно, амплитудно-частотная характеристика однозначно определяет передаточную функцию системы.

Зная характеристики звена, можно найти сигнал на его выходе при любом сигнале на входе. Действительно, любой сигнал может быть представлен в виде совокупности элементарных сигналов типа синусоиды, единич­ного скачка или единичного импульса. Для каждого же из этих простых сигналов, подаваемых на вход звена, может быть найден выходной сигнал. Применяя для линейных систем прин­цип наложения, можно рассматривать выходной сигнал как сово­купность составляющих, получающихся при рассмотрении мно­жества простых сигналов на входе звена.

Так, если входной сигнал задан частотным спектром 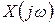, то частотный спектр сигнала на выходе находится с помощью комплексного коэффициента усиления звена

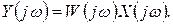(1.6.8)

Если входной сигнал задан изображением 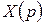, то изобра­жение сигнала на выходе находится с помощью передаточной функции

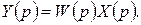(1.6.9)

Бели входной сигнал задан функцией времени 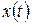, то сиг­нал на выходе звена может быть найден с помощью переход­ной функции или весовой.

Разлагая 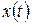на совокупность единичных скачков 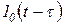по формуле (1.4.1) и находя реакцию звена на каждый из скач­ков, получаем

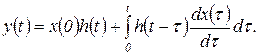(1.6.10)

Аналогично, разлагая 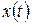на совокупность единичных импульсов 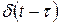по формуле (1.4.2) и находя реакцию звена на каждый из импульсов, получаем

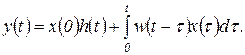(1.6.11)

Таким образом, рассмотренные характеристики звеньев дают полную возможность рассчитать сигнал на выходе звена, если известен сигнал на его входе при нулевых начальных условиях.

Если начальные условия ненулевые, то расчет несколько усложняется. В этом случае при расчете сигнала операторным методом следует исходить из формулы (1.4.10).

Соответствующим выбором начала отсчета времени при рас­чёте процессов, вызванных приращением x относительно началь­ного значения, можно свести к нулю .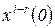

Однако начальные значения 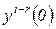необходимо учитывать. В этом случае из формулы (1.4.10) получаем

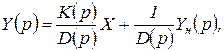(1.6.12)

где

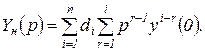(1.6.13)

Будем считать, что изображение типового воздействия 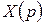— дробно-рациональная функция

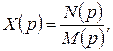(1.6.14)

где 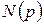и 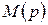— полиномы от р.

Тогда

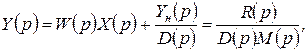(1.6.15)

где

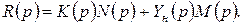(1.6.16)

При нулевых начальных условиях 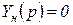и выражение (1.6.12) переходит в (1.6.9).

Согласно (1.6.15) ненулевые начальные условия изменяют лишь числитель изображения выходного сигнала. Корни же знаменателя (полюсы) этого изображения при любых начальных условиях определяются из уравнений:

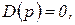(1.6.17)

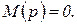(1.6.18)

Для определения оригинала 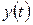можно воспользоваться разложением (1.6.12) на элементарные дроби, соответствующие n корням уравнения (1.6.17) и s корням уравнения (1.6.18).

Если все корни (1.6.17) и (1.6.18) различны, то

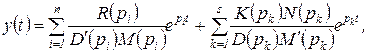(1.6.19)

где 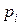— корни (1.6.17), 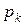— корни (1.6.18).

Компоненты первой суммы в (1.6.19) с точностью до коэф­фициентов определяются корнями уравнения (1.6.17) и для устой­чивых звеньев с течением времени затухают. Эта составляю­щая называется переходной (или свободной) составляющей процесса

(1.6.20)

В частности, при нулевых начальных условиях

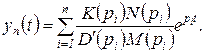(1.6.21)

Поскольку суммирование в (1.6.20) производит­ся с весовыми коэффициентами, зависящими от коэффициен­тов характеристического уравнения, числителя передаточной функции звена 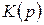, начальных условий 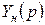и параметров воздействия 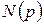и 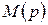(1.6.19), то протекание переходного процесса в целом существенно зависит от всех этих факторов.

Сравнительную оценку переходных процессов целесообраз­но вести для единых (стандартных) типовых воздействий при стандартных (обычно нулевых) начальных условиях.

Компоненты второй суммы в (1.6.19) с теми же оговорками определяются корнями уравнения (1.6.18) — полюсами изображе­ния рассматриваемого воздействия. Эта составляющая назы­вается вынужденной составляющей процесса

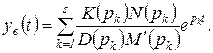(1.6.22)

Заметим, что вынужденная составляющая зависит от вход­ного воздействия и параметров передаточной функции системы, но не зависит от начальных условий .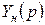

По истечении времени, достаточного для того, чтобы пере­ходная составляющая (1.6.20) успела затухнуть с требуемой точ­ностью, считают процесс установившимся.

При этом 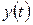в установившемся процессе определяется вынужденной составляющей и не зависит от начальных условий.

При наличии кратных корней уравнения (1.6.17) или (1.6.18) разложение на простые дроби следует вести с учётом крат­ности.