Регулярные сигналы

Любой сложный сигнал может быть представлен в виде со­вокупности более простых сигналов.

В качестве простейших сигналов будем пользоваться сле­дующими:

а) гармонический сигнал 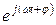или ;

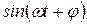б) единичный скачок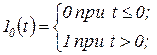

в) единичный импульс .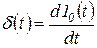

Пусть сигнал выражается некоторой функцией времени 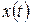. Тогда выражение его в виде совокуп­ности гармонических сигналов производится путем применения ряда Фурье для периодических сигналов и преобразования Фурье для непериодических сигналов.

Применяя интеграл Дюамеля в различной форме, этот сиг­нал можно представить также или в виде совокупности еди­ничных скачков

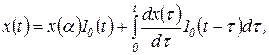(1.4.1)

при ;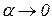

или в виде совокупности единичных импульсов

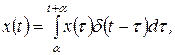(1.4.2)

где .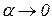

Графическая иллюстрация к интегралам (1.4.1) и (1.4.2) при­ведена на рисунке 1.4.2. Здесь 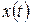представляется в виде совокупности скачков величиной 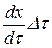, действующих в моменты τ при (рисунок 1.4.2, а), или в виде интеграла от δ-функции, умножаемой на значение х в момент времени τ (рисунок 1.4.2, б).

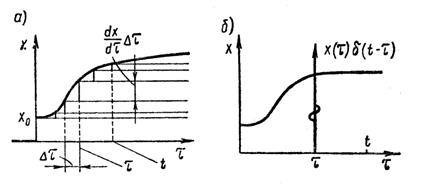
Рисунок 1.4.2 – Геометрическая иллюстрация разложения сигнала

В общем случае обыкновенное дифференциальное уравне­ние простого (односвязного) звена, выражающее зависимость между входным сигналом х и выходным сигналом у, записы­вается следующим образом:

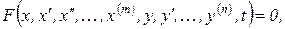(1.4.3)

где

и .

Для систем с параметрами, не изменяющимися во времени, функция F не зависит от t.

Для линейных систем функция F выражается линейной зависимостью и уравнение (1.4.3) принимает следующий вид:

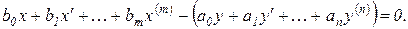(1.4.4)

При гладкой зависимости функции F от её аргументов и малых изменениях аргументов нелинейное уравнение, связы­вающее х и у, может быть приведено к линейному.

Пусть при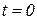

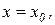
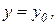
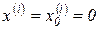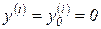и при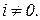

Тогда уравнение (1.4.3) приобретает вид

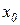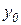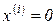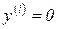Разложив функцию F в ряд Тейлора в окрестности точек , и , для 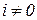и пренебрегая высшими членами разложения для и 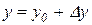, получим

(1.4.5)

где

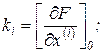
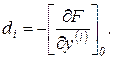
При этом предполагается, что и знак F выбирается таким, чтобы .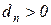

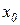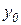Если теперь за начало отсчета х и у принять точки и , то уравнение (1.5) можно записать так

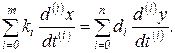(1.4.6)

Здесь под x и y понимаются их указанные выше прираще­ния 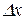и .

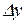Переходя от оригиналов к их изображениям по Лапласу, получаем:

(1.4.7)

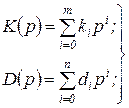(1.4.8)

и, соответственно, зависимость между частотными спектрам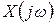и и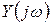

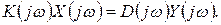(1.4.9)

Если решается задача с ненулевыми начальными условиями и в момент 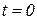как x и у, так и их производные могут быть отличны от нуля, то переход от оригинала к изображе­нию в уравнении (1.4.6) даёт

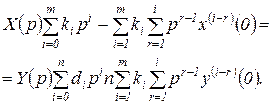(1.4.10)

Большинство задач, рассматриваемых в теории регулиро­вания с помощью принципа наложения, сводится к решению задач с нулевыми начальными условиями. Этому также спо­собствует рассмотрение каждого воздействия как сигнала, который начинает действовать только при 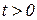, а при 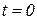он сам и его производные равны нулю. Разумеется, при этом необходимо учитывать разрывы функции, имеющие место сразу же при переходе от нуля в область, где .

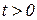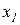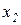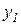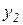Для сложных (многосвязных) звеньев может быть приме­нена аналогичная линеаризация уравнений. В этом случае, в зависимости от количества входных и выходных сигналов, звено описывается системами уравнений типа (1.4.3), (1.4.6), (1.4.7). Так, например, если звено имеет два входных сигнала и и два выходных и , то уравнение (1.4.7) при­обретает вид системы уравнений:

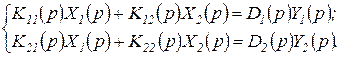(1.4.11)