Связь преобразований Фурье и Лапласа

Основные понятия операционного исчисления. Преобразование Фурье и Лапласа

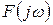Прямое и обратное преобразования Фурье. Совокупность операций, позволяющих по заданной функции находить ей соответствую­щую спектральную характеристику , называется преобразова­нием Фурье и описывается следующим выражением:

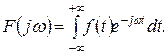(1.3.1)

Интеграл в правой части равенства (1.3.1) понимается в смысле главного значения, т.е.

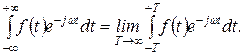(1.3.2)

Равенство (1.3.1) устанавливает связь между функцией , аргументом которой служит время t, и ей соответствующей комплексной функ­цией 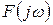, имеющей в качестве аргумента частоту ω.

Формула интеграла Фурье

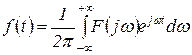(1.3.3)

позволяет по известной функции 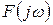определить ей соответствую­щую функцию , и называется формулой обратного преобразования Фурье.

Интеграл в правой части равенства (1.3.3) также следует рассмат­ривать в смысле главного значения, т.е.

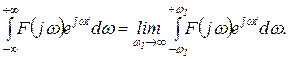(1.3.4)

В ряде задач автоматического регулирования функция харак­теризует процесс, имеющий место лишь начиная с некоторого вре­мени t, который можно принять за нулевой. В этом случае 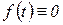при 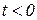и формула (1.3.1) принимает вид

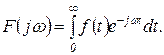(1.3.5)

Преобразование, определяемое формулой (1.3.5), называется прямым односторонним преобразованием Фурье.

Обратное преобразование Фурье, соответствующее прямому одно­сто­рон­нему преобразованию, остается двусторонним по переменной ω и даётся равенством

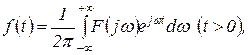(1.3.6)

где 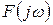определяется формулой (1.3.5).

Одностороннему преобразованию Фурье могут быть подвергнуты те функции , которые в любом интервале, заключенном в пределах 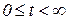, удовлетворяют условиям Дирихле, и интеграл 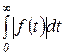существует.

Прямое и обратное преобразование Лапласа. Рассмотрим функцию вещественной переменной t, при этом будем предпо­лагать выполненными следующие условия:

1) Функция непрерывна для всех значений 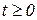. Непре­рывность может быть нарушена лишь в отдельных точках, являю­щихся точками разрыва непрерывности первого рода, причем число этих точек должно быть конечным на любом интервале ограничен­ной длины.

2) Функция 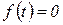для значений .

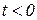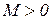3) Функция имеет ограниченный порядок возрастания, т.е. можно указать такие постоянные числа и 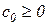, при кото­рых выполняется неравенство

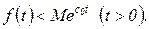
Число 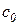является показателем роста функции . Функция , удовлетворяющая условиям 1–3, называется оригиналом. Многие функции, встречающиеся при описании процессов в автоматических системах, являются оригиналами. Например, оригиналами будут функции 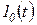; ; 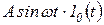; 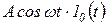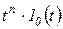( 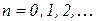); ; 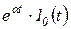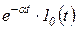( 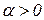) и ряд других функций. Наличие в этих функциях множителя — единичной ступенчатой функции 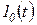— обе­спечивает выполнение второго условия, т.е. обращение функции в ноль при 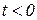. С физической точки зрения это условие является вполне естественным. Действительно, в автоматических сис­темах обычно представляют интерес процессы, начинающиеся с не­которого момента времени. Например, если функция характери­зует отклонение регулируемой величины, происходящее при прило­жении к системе в момент 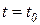возмущающего воздействия, то очевидно, что при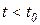 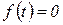, так как реакция на возмущение не может возникнуть ранее момента времени приложения, к системе самого возмущения. Этот момент времени может быть принят за нулевой момент, т.е. можно полагать, что 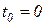; тогда при 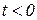получим 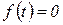. Условие 2 поэтому, естественно, учитывает началь­ные условия, в которых находится автоматическая система. Как правило, условия 1 и 3 также выполняются для большинства функ­ций , характеризующих процессы в автоматических системах. Если хотя бы одно из условий 1–3 не выполняется, то функция не будет являться оригиналом. Согласно условию 1 ори­гинал не может обращаться в бесконечность при 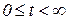, поэтому не является оригиналами функция 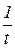, 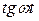. Не является оригиналом также функция 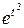, поскольку для этой функции не выполнено условие 3: функция 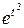при возрастает быстрее, чем возрастает функция .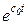

Функция 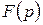комплексного переменного 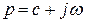, определяе­мая равенством

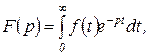(1.3.7)

называется изображением функции по Лапласу. Интеграл в правой части равенства (1.3.7) называется интегралом Лапласа. Этот несобственный интеграл по определению равен

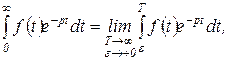(1.3.8)

причем 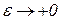означает правый предельный переход.

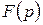С помощью интеграла Лапласа устанавливается соответствие между функцией и её изображением . Символически преобразование Лапласа записывается в виде

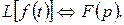(1.3.9)

Интеграл Лапласа будет сходящимся, если существует предел в правой части равенства (1.3.8).

Для перехода от изображения 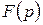к ему соответствующему оригиналу необходимо выполнить обратное преобразование Лапласа. Оригинал в точках непрерывности опреде­ляется равенством

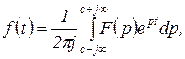(1.3.10)

где 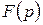— изображение по Лапласу оригинала , а интеграл в пра­вой части этого равенства понимается в смысле главного значения, т.е.

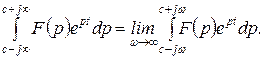(1.3.11)

Формула (1.3.10) называется формулой обращения. С её помощью устанавливается связь между изображением 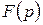и ему соответст­вующим оригиналом . Процесс получения оригинала по задан­ному изображению 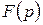представляет собой обратное преобразование Лапласа. Символи­чески обратное преобразование Лапласа записывают в виде

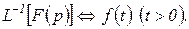(1.3.12)

Условие 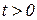учитывает то обстоятельство, что оригинал 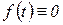при .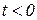

Наиболее часто встречающиеся оригиналы и соответствующие им приложения приведены в Приложении 1.

Связь преобразований Фурье и Лапласа

Формула (1.3.7) прямого преобразования Лапласа может рассматриваться как результат определенным образом построенного обобщения одностороннего пре­образования Фурье. Пусть, например, функция удовлетворяет условиям Дирихле в интервале 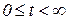, причем 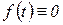при .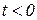

Преобразование Фурье может быть применено к функциям , для которых интеграл 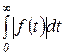существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе про­цессов в автоматических системах, например функции 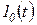; ; 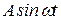; 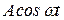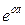(при действительном 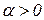); t и др. Для того чтобы иметь возможность подобную функцию преобразовать по Фурье, предварительно её надо умножить на множитель 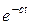, где вещест­венное число 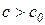выбрано таким образом, чтобы интеграл

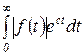
был сходящимся. Значение 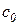для каждой функции является вполне определенным. Используя формулу прямого одностороннего преобразования Фурье

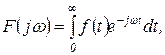
будем преобразовывать по Фурье не функцию , а функцию 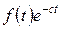, удовлетворяющую условиям применения этого преобразо­вания:

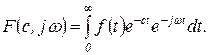(1.3.13)

Введя новую комплексную переменную 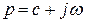, получим:

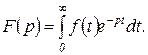
Это выражение представляет собой формулу (1.3.7) прямого преобра­зования Лапласа.

Таким образом, преобразование Лапласа является результатом распространения преобразования Фурье на функции, которые, удов­летворяя условиям Дирихле в интервале 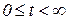, не удовлетво­ряют в этом интервале условию абсолютной интегрируемости.

Рассмотрим теперь формулу обратного преобразования Фурье

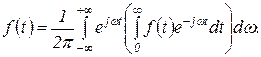
Заменив в левой и правой частях этого равенства на 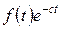, получим

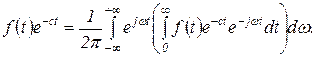
Учитывая, что 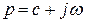, , 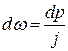найдем

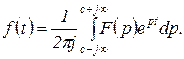
Это равенство, как видно из (1.3.10), является формулой обратного преоб­разования Лапласа.

Таким образом, обратное преобразование Лапласа может рас­сматри­ваться как развитие обратного преобразования Фурье.