Автоколебательные системы

Автоколебания представляют собой незатухающие колебания в нелинейной диссипативной системе, поддерживающиеся за счет поступления энергии от внешнего источника. При этом параметры колебаний (форма, амплитуда, частота) определяются свойствами самой колебательной системы, а не периодическим внешним воздействием, как в случае вынужденных колебаний.

Упрощенная схема автоколебательной системы приведена на рисунке 19.1. Система содержит колебательное звено 1, которое определяет частоту автоколебаний. Часть энергии колебаний отводится в цепь обратной связи, где усиливается усилительным элементом 2, а затем вновь возвращается в колебательное звено. Усиление колебаний происходит за счет источника энергии 3. Цепь обратной связи содержит нелинейный элемент 4, который регулирует поступление энергии от источника 3, обеспечивая устойчивость работы автоколебательной системы.

Рассмотрим в качестве примера схему, изображенную на рисунке 19.2 (генератор Ван дер Поля). Колебательный контур состоит из катушки индуктивности 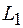с активным сопротивлением 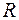и конденсатора 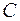. Напряжение на обкладках конденсатора подается на сетку триода Л. Анодно-сеточная характеристика триода (за висимость тока в анодной цепи от напряжения на сетке 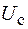) имеет вид, изображенный на рисунке 19.3. Если потенциал сетки по отношению к катоду положительный, то в промежутке "сетка–катод" создается ускоряющее электрическое поле, под действием которого электроны, вылетающие с катода в результате термоэлектронной эмиссии, движутся к аноду, пролетают сквозь сетку и попадают на анод. Когда потенциал сетки по отношению к катоду отрицательный, между сеткой и катодом возникает тормозящее электрическое поле, которое препятствует движению электронов к аноду. Так как сетка расположена ближе к катоду, чем анод, то малое изменение напряжения на сетке сильно влияет на анодный ток, т. е. триод работает как усилительный элемент.

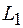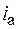В анодную цепь триода включена катушка индуктивности , которая индуктивно связана с катушкой . Вследствие явления взаимной индукции при изменении тока, протекающего через катушку (т. е. анодного тока ), в катушке 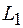будет наводиться ЭДС взаимной индукции. Эта ЭДС в зависимости от способа включения катушек (согласного или несогласного) будет либо усиливать колебания в контуре, либо ослаблять их.

Если в колебательном контуре каким-либо образом возбуждены гармонические колебания, то часть энергии этих колебаний после усиления триодом будет возвращаться в колебательную систему через индуктивно связанные катушки, обеспечивая тем самым обратную связь. Если дополнительная энергия, подводимая по цепи обратной связи, усиливает колебания в контуре, то такая связь называется положительной, а если колебания ослабляются, то связь называется отрицательной. При положительной обратной связи по второму закону Кирхгофа для колебательного контура можно записать

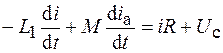, (19.1)

где 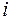– сила тока в контуре; 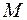– взаимная индуктивность катушек.

Уравнение (19.1) отличается от рассмотренного ранее дифференциального уравнения затухающих колебаний тем, что в нем кроме ЭДС самоиндукции учтена также ЭДС взаимной индукции 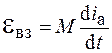. При малой амплитуде колебаний ток в анодной цепи пропорционален напряжению на сетке (линейное приближение), т. 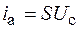е. , где 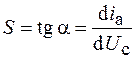– коэффициент пропорциональности. Напряжение на конденсаторе и ток в колебательном контуре связаны с зарядом на обкладках конденсатора соотношениям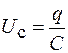и и 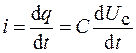. С учетом этого уравнение (19.1) примет вид

.

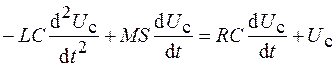Поделив обе части уравнения на 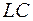, после элементарных преобразований приведем его к виду

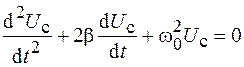, (19.2)

где обозначено 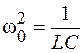и

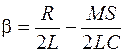. (19.3)

Уравнение (19.2) совпадает с дифференциальным уравнением затухающих колебаний, а его решение будет иметь вид

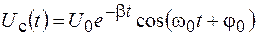. (19.4)

Из (19.3) следует, что если

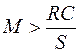, (19.5)

то коэффициент затухания 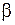будет отрицательным, т. е. амплитуда колебаний в такой системе неограниченно возрастает (рис. 19.4).

Возбуждение колебаний произойдет в результате усиления шумов, которые присутствуют в любой электрической цепи. Хаотическое тепловое движение электронов проводимости приведет к случайным изменениям напряжения на конденсаторе. В радиотехнике такие случайные флуктуации называются шумами. Спектр шумов очень широкий и в нем всегда найдутся случайные колебания, частота которых совпадает с резонансной частотой. Именно эти флуктуации будут усиливаться за счет положительной обратной связи.

Из рисунка 19.3 видно, что линейность характеристики триода обеспечивается лишь в ограниченном диапазоне изменения напряжения на сетке. Как только колебания достигнут области насыщения и отсечки, дальнейшее нарастание амплитуды прекратится, и в системе установятся незатухающие колебания с некоторой постоянной амплитудой, величина которой будет определяться не начальными условиями, а собственными характеристиками системы. Особенностью автоколебаний является то, что их частота и амплитуда, в отличие от вынужденных колебаний, определяются параметрами самой колебательной системы, а не внешним воздействием. При этом наличие в системе нелинейного элемента имеет принципиальное значение, так как именно он ограничивает процесс нарастания амплитуды колебаний и делает колебательную систему устойчивой.

На фазовой диаграмме установившимся колебаниям будет соответствовать некоторая замкнутая фазовая траектория, по которой движется изображающая точка (на рис. 19.5 она показана жирной линией). Эта траектория называется предельным циклом,или аттрактором (от английского – to attract – притягивать). Процесс самовозбуждения колебаний на фазовой плоскости изображается раскручивающейся спиралью 1. Если амплитуда колебаний превы 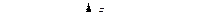сит установившееся значение, то это приведет к возрастанию потерь, в результате чего амплитуда колебаний вновь уменьшится до установившегося значения. На фазовой плоскости этот процесс изображен спиралью 2, накручивающейся на предельный цикл. Таким образом, режим установившихся колебаний является устойчивым к возмущениям, и эта устойчивость обеспечивается нелинейностью колебательной системы.

Процесс самовозбуждения можно рассматривать как пример самоорганизации в нелинейной системе, в которой одновременно протекают два процесса: диссипация (рассеяние) энергии и ее поступление от внешнего источника. Такие системы называются открытыми диссипативными системами. Независимо от начального состояния, которое является случайным, колебательная система в ходе эволюции переходит в упорядоченное состояние (установившиеся колебания), которое является устойчивым. На фазовой плоскости это отражается в том, что все фазовые траектории, начинающиеся из любой точки, притягиваются к аттрактору (предельному циклу). В более сложных нелинейных системах возможно существование нескольких аттракторов, для каждого из которых существует своя область притяжения и тогда в зависимости от случайных начальных условий (или в результате какого-либо внешнего воздействия) система может перейти в одно из возможных устойчивых упорядоченных состояний. Изучение таких нелинейных систем составляет предмет нелинейной динамики, которая активно развивается в последние десятилетия. В ходе ее развития были открыты нелинейные системы, которым соответствуют так называемые странные аттракторы. Они отличаются от обычных аттракторов тем, что при любом сколь угодно малом воздействии на систему (или неточности в определении начальных условий) ее эволюция может идти различными путями и в результате прогноз (предсказание) поведения системы может быть только вероятностным. Подобное поведение свойственно не только нелинейным физическим системам, оно наблюдается при протекании химических реакций, в ходе эволюции живой и неживой природы, в социальной сфере и т. д. Это привело к возникновению на основе нелинейной динамики новой междисциплинарной науки – синергетики, которая занимается изучением открытых диссипативных систем самой различной природы.