Понятие о связанных гармонических осцилляторах.

Нормальные колебания (моды)

Рассмотренные примеры свободных колебаний относились к колебательным системам с одной степенью свободы, т. е. к системам, состояние которых однозначно определяется одной независимой физической величиной (смещением тела от положения равновесия, зарядом на обкладках конденсатора и т. п.). В более сложных колебательных системах их состояние может определяться несколькими независимыми величинами. Колебательные системы, состояние которых определяется n независимыми физическими величинами, называютсясистемами с несколькими степенями свободы. Число n называется числом степеней свободы колебательной системы.

На рисунке 16.1 приведены примеры систем с двумя степенями свободы. Каждая колебательная система, показанная на рисунке, представляет собой как бы два осциллятора, которые взаимодействуют между собой, поэтому их называютсвязанными гармоническими осцилляторами.

Систему связанных осцилляторов, изображенную на рисунке 16.2 можно рассматривать как механическую модель кристаллической решетки, в узлах которой расположены атомы. Между атомами действуют упругие силы, удерживающие их в узлах решетки. Атомы совершают тепловые колебания вблизи положения равновесия. Если число атомов в кристаллической решетке равно 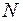и при этом каждый атом совершает колебания вдоль трех координатных осей, то кристаллическую решетку можно рассматривать как систему связанных осцилляторов с 3 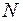степенями свободы.

Колебания связанных осцилляторов с 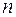степенями свободы описываются системой 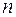дифференциальных уравнений. При отсутствии потерь ее общим решением является линейная комбинация 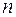гармонических колебаний:

. (16.1)

Каждое отдельное гармоническое колебание в выражении (16.1) называется собственным типом колебаний, или модой. Таким образом, колебания связанных осцилляторов можно представить в виде суперпозиции мод, число которых равно числу степеней свободы 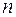колебательной системы. Каждая мода имеет определенную частоту, зависящую от параметров системы. Амплитуды и начальные фазы каждой моды определяются начальными условиями.

В качестве иллюстрации рассмотрим колебания связанных осцилляторов, изображенных на рисунке 16.2. Будем считать, что массы грузов и жесткости пружин одинаковы. Решение дифференциальных уравнений для показывает, что в такой системе существуют 2 моды с частотам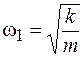и и 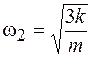. При возбуждении первой моды с частотой 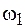обе частицы совершают синхронные колебания с этой частотой, причем амплитуды и начальные фазы колебаний равны. При этом средняя пружина, обеспечивающая упругую связь частиц, не испытывает растяжения (рис. 16.3, а). При возбуждении второй моды обе частицы совершают колебания с частотой 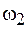и с одинаковой амплитудой, но в противофазе (рис. 16.3, б). Любое другое колебание в системе может быть представлено в виде суперпозиции этих двух собственных типов колебаний.

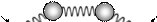Если ослабить связь между осцилляторами, уменьшив жесткость средней пружины, то частоты мод будут близки друг другу и возникнут биения. Колебания будут выглядеть таким образом, что связанные осцилляторы обмениваются энергией. Если в начальный момент в системе, изображенной на рисунке 16.3, отклонить левый груз, а затем отпустить, то вначале возникнут колебания этого груза, а второй будет оставаться практически неподвижным. Постепенно амплитуда колебаний первого груза будет уменьшаться, а второй начнет раскачиваться, т. е. энергия колебаний перейдет от одного осциллятора к другому. Далее этот процесс обмена энергией будет периодически повторяться с частотой биений.

При увеличении количества грузов соответственно увеличивается число мод, каждая из которых характеризуется собственной частотой. При возбуждении в системе одной моды все частицы совершают колебания с частотой этой моды, а разность фаз колебаний любой пары частиц остается неизменной во времени. На рисунке 16.4 схематически показаны моды колебаний для грузов, связанных пружинами. Из рисунка видно, что по мере увеличения числа степеней свободы конфигурация мод все более становится похожа на волны, причем для каждой моды на длине системы укладывается целое число полуволн. Этот важный вывод понадобится при рассмотрении электромагнитных волн в двухпроводной линии и тепловых колебаний кристаллической решетки.

Понятие моды широко используется для анализа не только колебательных, но и волновых процессов. Совокупность мод колебательной системы играет роль базиса, по которому производится разложение произвольного процесса. Здесь можно провести следующую аналогию. Из векторной алгебры известно, что в трехмерном пространстве произвольный вектор 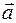можно представить в виде линейной комбинации единичных базисных векторов (ортов):

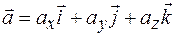. (16.2)

Колебательный (или волновой) процесс описывается некоторой функцией, которую, подобно вектору, можно представить в виде линейной комбинации базисных функций – совокупности мод колебательной системы. Продолжая аналогию с векторами, можно представить функциональное пространство, размерность которого равна числу степеней свободы колебательной системы 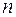. Моды аналогичны ортам соответствующих координатных осей и образуют базис функционального пространства. Размерность и базис функционального пространства определяются свойствами колебательной системы. Любой процесс в колебательной системе можно мысленно изобразить в виде псевдовектора в этом 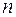-мерном функциональном пространстве и представить как линейную комбинацию "ортов" (мод) координатных осей. При этом амплитуды мод аналогичны проекциям вектора на соответствующие координатные оси и определяются начальными условиями. Модальное разложение колебательных и волновых процессов используется так же широко, как и разложение векторов по ортам координатных осей.