Элементы Фурье-анализа

Пусть имеются два связанных 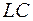-контура, как это изображено на рисунке 16.1, г. Они представляют собой колебательную систему с двумя степенями свободы и, так же, как и для грузов на пружине, колебания силы тока в каждом из них можно представить в виде суммы двух гармонических колебаний с частотами 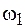и .

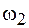Возьмем третий контур и, используя явление взаимной индукции, отведем часть энергии колебаний в этот контур через индуктивно связанные катушки и 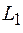, как показано на рисунке 17.1. Дополнительный контур содержит конденсатор переменной емкости 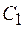. Изменяя емкость конденсатора, можно изменять частоту 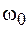собственных колебаний в этом контуре. Напряжение на конденсаторе 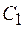измеряется с помощью вольтметра или осциллографа.

При возбуждении в связанных контурах колебаний в 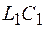-контуре в результате явления взаимной индукции будет наводиться ЭДС взаимной индукции и возникнут вынужденные колебания. Если частота собственных колебаний 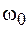сильно отличается от частот 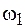и 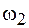, то амплитуда вынужденных колебаний будет очень мала. По мере приближения частоты собственных колебаний 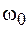к частоте 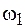амплитуда будет расти и достигнет максимального значения, когда эти частоты совпадут. Наступит явление резонанса на частоте 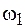. Увеличивая далее частоту собственных колебаний 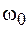, можно вновь наблюдать явление резонанса, когда она станет равной 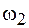. При дальнейшем увеличении частоты 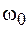амплитуда вынужденных колебаний станет практически равной нулю. Таким образом, перестраивая частоту собственных колебаний 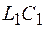-контура и наблюдая изменение напряжения на конденсаторе 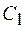, можно вполне однозначно определить, что колебания в связанном осцилляторе представляют суперпозицию двух гармонических колебаний с частотам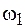и и .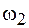

Представление некоторого изменяющегося во времени процесса 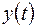в виде суперпозиции (линейной комбинации) гармонических колебаний с различными частотами называется спектральным разложением. Гармонические колебания, на которые раскладывается сложный сигнал, называются спектральными компонентами, или гармониками. График зависимости амплитуды спектральных компонентов от частоты называется спектром сигнала.

Используя приведенную терминологию, можно сказать, что 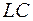-контур позволяет осуществлять спектральное разложение сложных временных процессов (сигналов), т. е. 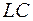-контур можно использовать как спектральный прибор. Колебательный контур является наиболее удобным устройством для спектрального анализа электрических сигналов и широко применяется в радиотехнике. Однако можно утверждать, что любой гармонический осциллятор может использоваться для этих целей, если имеется техническая возможность плавно изменять частоту собственных колебаний.

Возникает вопрос: каким условиям должна удовлетворять произвольная функция 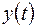, чтобы ее можно было представить в виде суперпозиции гармоник, и сколькими способами это можно сделать? Другими словами: можно ли любой сигнал 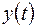разложить в спектр и будет ли это разложение единственным? Ответы на эти вопросы, а также методы разложения составляют предмет специального раздела математики, называемого гармоническим анализом,или Фурье-анализом. В математике строго доказываются теоремы о существовании и единственности разложения в спектр, разработаны методы разложения, основанные на преобразовании Фурье. Не вдаваясь в подробности, отметим, что любой физически реализуемый процесс может быть разложен в спектр. Для периодических сигналов этот спектр представляет совокупность дискретных гармоник (его называют линейчатым спектром). Для непериодических сигналов спектр сплошной.

Вопросы для самоконтроля

1. При каком условии колебания будут гармоническими?

2. Запишите дифференциальное уравнение гармонических колебаний и его решение.

3. От чего зависят: а) частота гармонических колебаний; б) период; в) амплитуда; г) начальная фаза?

4. Получите уравнение фазовой траектории гармонического осциллятора в явном виде.

5. Что такое биения?

6. При каких условиях можно наблюдать фигуры Лиссажу?

7. Запишите дифференциальное уравнение затухающих колебаний и его решение.

8. Проанализируйте изменение характеристик затухания в зависимости от параметров 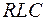-контура.

9. На рисунке представлены два колебания 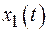и 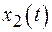. Сравните: а) коэффициенты затухания; б) логарифмические декременты; в) добротности.

10. Чем будут отличаться вынужденные колебания в двух колебательных контурах, имеющих одинаковые индуктивности и емкости 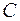, но разные добротности?

11. В чем заключается явление резонанса?

12. Как изменится резонансная кривая 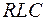-контура, если в него включить последовательно дополнительное сопротивление?

13. Что такое моды колебательной системы? Чем определяется их количество?

Глава 2. АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ