Явление резонанса
По истечении времени, много большего времени установления колебаний 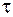 , переходный процесс завершается, и в колебательной системе происходят установившиеся (стационарные) вынужденные колебания под действием внешнего воздействия. В этом случае в общем решении (13.1) первым слагаемым можно пренебречь и тогда
, переходный процесс завершается, и в колебательной системе происходят установившиеся (стационарные) вынужденные колебания под действием внешнего воздействия. В этом случае в общем решении (13.1) первым слагаемым можно пренебречь и тогда
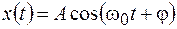 , (14.1)
, (14.1)
где амплитуда 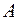 и сдвиг фазы
и сдвиг фазы 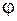 определяются выражениями (12.13), (12.14). Из этих выражений следует, что амплитуда и фаза зависят от частоты внешнего воздействия. График зависимости амплитуды вынужденных колебаний от частоты
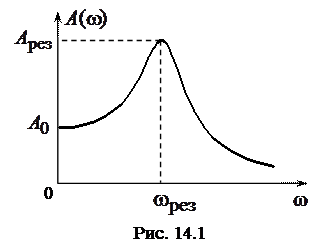
определяются выражениями (12.13), (12.14). Из этих выражений следует, что амплитуда и фаза зависят от частоты внешнего воздействия. График зависимости амплитуды вынужденных колебаний от частоты 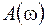 называется резонансной кривой и приведен на рисунке 14.1. Если частота равна нулю, т. е. система подвергается статическому внешнему воздействию (постоянная сила в случае пружинного маятника, постоянная ЭДС в
называется резонансной кривой и приведен на рисунке 14.1. Если частота равна нулю, т. е. система подвергается статическому внешнему воздействию (постоянная сила в случае пружинного маятника, постоянная ЭДС в 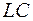 -контуре и т. п.), то из (12.9) следует
-контуре и т. п.), то из (12.9) следует
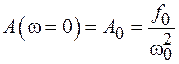 . (14.2)
. (14.2)
Для пружинного маятника 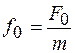 и
и 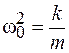 , поэтому
, поэтому 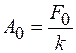 , т. е. при нулевой частоте внешней силы груз испытывает статическое смещение
, т. е. при нулевой частоте внешней силы груз испытывает статическое смещение
 .
.
Если частота внешнего воздействия неограниченно возрастает 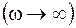 , то из (12.13) следует, что амплитуда вынужденных колебаний стремится к нулю.
, то из (12.13) следует, что амплитуда вынужденных колебаний стремится к нулю.
Как видно из рисунка 14.1, при увеличении частоты внешнего воздействия от нуля амплитуда колебаний сначала увеличивается, а затем, достигнув некоторого максимального значения, асимптотически стремится к нулю. Явление увеличения амплитуды вынужденных колебаний при изменении частоты внешнего воздействия называется явлением резонанса, а частота, при которой амплитуда имеет максимальное значение, называется резонансной.
 Чтобы найти резонансную частоту, необходимо исследовать на экстремум выражение (12.13). Так как числитель выражения от частоты не зависит, то экстремумы функции
Чтобы найти резонансную частоту, необходимо исследовать на экстремум выражение (12.13). Так как числитель выражения от частоты не зависит, то экстремумы функции 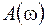 совпадают с экстремумами знаменателя выражения (12.13). Приравнивая нулю первую производную от знаменателя, получим
совпадают с экстремумами знаменателя выражения (12.13). Приравнивая нулю первую производную от знаменателя, получим
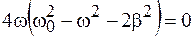 .
.
Данное уравнение имеет два корня 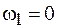 и
и  . Легко убедиться, что максимум амплитуды достигается при втором значении корня, поэтому резонансная частота
. Легко убедиться, что максимум амплитуды достигается при втором значении корня, поэтому резонансная частота
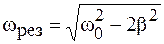 . (14.3)
. (14.3)
Из полученного выражения следует, что резонансная частота всегда меньше частоты собственных колебаний 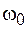 . При увеличении потерь энергии в системе резонансная частота уменьшается. При малом затухании
. При увеличении потерь энергии в системе резонансная частота уменьшается. При малом затухании 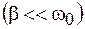 , т. е. при высокой добротности колебательной системы, различием частот можно пренебречь и считать, что резонанс в системе наступает при совпадении частоты внешнего воздействия с частотой собственных колебаний.
, т. е. при высокой добротности колебательной системы, различием частот можно пренебречь и считать, что резонанс в системе наступает при совпадении частоты внешнего воздействия с частотой собственных колебаний.
Подставив найденное значение резонансной частоты в выражение (12.13), получим амплитуду вынужденных колебаний при резонансе:
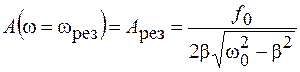 . (14.4)
. (14.4)
Из последнего выражения следует, что при уменьшении потерь 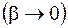 амплитуда при резонансе неограниченно увеличивается
амплитуда при резонансе неограниченно увеличивается 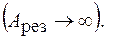 Поделив (14.4) на (14.2), можно показать, что при малом затухании
Поделив (14.4) на (14.2), можно показать, что при малом затухании 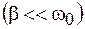 отношение амплитуды вынужденных колебаний на резонансной частоте к амплитуде на нулевой частоте равно добротности колебательной системы:
отношение амплитуды вынужденных колебаний на резонансной частоте к амплитуде на нулевой частоте равно добротности колебательной системы:
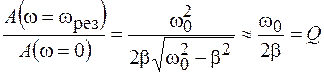 . (14.5)
. (14.5)
Сделанный вывод позволяет легко определить добротность колебательной системы по экспериментально полученной резонансной кривой.
 Резонансные свойства колебательной системы принято характеризовать шириной резонансной кривой. На резонансной частоте колебательная система обладает наибольшим запасом энергии, которая пропорциональна квадрату амплитуды колебаний. Шириной резонансной кривой называется разность частот, на которых энергия колебаний уменьшается в 2 раза по сравнению с максимальной. Уменьшению энергии в 2 раза соответствует уменьшение амплитуды колебаний в
Резонансные свойства колебательной системы принято характеризовать шириной резонансной кривой. На резонансной частоте колебательная система обладает наибольшим запасом энергии, которая пропорциональна квадрату амплитуды колебаний. Шириной резонансной кривой называется разность частот, на которых энергия колебаний уменьшается в 2 раза по сравнению с максимальной. Уменьшению энергии в 2 раза соответствует уменьшение амплитуды колебаний в 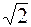 раз, поэтому ширина резонансной кривой определяется по уровню
раз, поэтому ширина резонансной кривой определяется по уровню 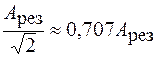 (рис. 14.2).
(рис. 14.2).
Можно показать, что при малых потерях
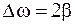 . (14.6)
. (14.6)
Так как 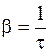 , то последнее выражение можно записать в виде
, то последнее выражение можно записать в виде
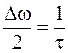 , (14.7)
, (14.7)
т. е. ширина резонансной кривой обратно пропорциональна времени релаксации (времени установления колебаний). Найдем с учетом (3.5), (10.8), (10.11) отношение частоты собственных колебаний 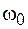 к ширине резонансной кривой:
к ширине резонансной кривой:
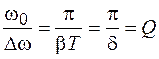 .
.
Так как при малых потерях в системе резонансная частота практически совпадает с собственной частотой, то добротность колебательной системы равна отношению резонансной частоты к ширине резонансной кривой, т. е.
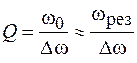 . (14.8)
. (14.8)
 Из (14.8) следует, что чем выше добротность колебательной системы (а значит, чем меньше коэффициент затухания и потери), тем уже резонансная кривая.
Из (14.8) следует, что чем выше добротность колебательной системы (а значит, чем меньше коэффициент затухания и потери), тем уже резонансная кривая.
График зависимости фазы вынужденных колебаний от частоты приведен на рисунке 14.3. Из (12.14) видно, что при 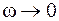 фаза
фаза  также стремится к нулю, т. е. на низких по сравнению с резонансной частотах колебания происходят в фазе с внешним воздействием. По мере увеличения частоты разность фаз увеличивается и на резонансной частоте
также стремится к нулю, т. е. на низких по сравнению с резонансной частотах колебания происходят в фазе с внешним воздействием. По мере увеличения частоты разность фаз увеличивается и на резонансной частоте 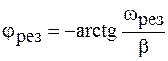 . Это следует из (12.14) после подстановки резонансной частоты (14.3). Если добротность системы велика
. Это следует из (12.14) после подстановки резонансной частоты (14.3). Если добротность системы велика 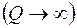 , то
, то 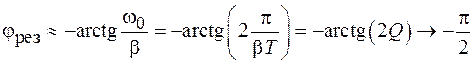 . При дальнейшем увеличении частоты сдвиг фазы возрастает и при
. При дальнейшем увеличении частоты сдвиг фазы возрастает и при 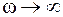 стремится к
стремится к 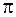 , т. е. на частотах, значительно превышающих резонансную частоту, колебания происходят в противофазе с внешним воздействием. Именно по этой причине амплитуда вынужденных колебаний на высоких частотах стремится к нулю.
, т. е. на частотах, значительно превышающих резонансную частоту, колебания происходят в противофазе с внешним воздействием. Именно по этой причине амплитуда вынужденных колебаний на высоких частотах стремится к нулю.
Дата добавления: 2015-08-08; просмотров: 2354;
