Электрические затухающие колебания

Рассмотрим, как будут выглядеть полученные результаты применительно к 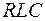-контуру, изображенному на рисунке 9.1. В этом случае функция описывает изменение заряда на обкладках конденсатора, т. е. .

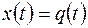Если потери в контуре, определяемые активным сопротивлением, достаточно малы, то в контуре будут происходить затухающие колебания. Это будет иметь место, если сопротивление 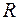меньше некоторого критического сопротивления , определяемого условием (10.1). Подставляя выражения для 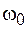, 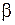и решая полученное уравнение относительно 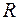, получим

. (11.1)

Если это условие выполнено, то из (10.4) находим, что частота затухающих колебаний

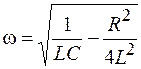. (11.2)

При этом заряд на обкладках конденсатора будет изменяться в соответствии с выражением

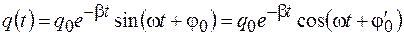, (11.3)

где начальные амплитуда 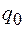и фаза 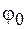или 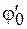определяются начальными условиями.

Из (10.8) следует, что логарифмический декремент затухания

(11.4)

и возрастает прямо пропорционально величине активного сопротивления. Из (10.11) легко получить выражение для добротности 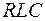-контура:

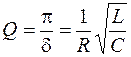. (11.5)

Последнее выражение показывает, что при увеличении сопротивления контура его добротность снижается.

Если величина сопротивления 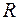становится больше критического сопротивления , то колебания в контуре прекращаются и процесс становится апериодическим.