И его решение. Если на колебательную систему действует периодическое внешнее воздействие, то возникающие в ней колебания называются вынужденными

Если на колебательную систему действует периодическое внешнее воздействие, то возникающие в ней колебания называются вынужденными. Из математики известно, что любой периодический процесс можно представить в виде суперпозиции гармоник (Фурье-спектр сигнала). Поэтому рассмотрим подробнее воздействие на колебательную систему гармонического внешнего воздействия вида

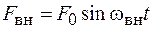, (12.1)

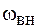где и соответственно амплитуда и частота внешнего воздействия.

Если колебательная система линейная (т. е. описывается линейным дифференциальным уравнением), то для нее выполняется принцип суперпозиции и ее реакция на произвольное периодическое воздействие может быть представлена в виде суперпозиции откликов на составляющие гармоники вида (12.1).

Чтобы получить дифференциальное уравнение вынужденных колебаний, обратимся к рассмотренным выше колебательным системам: груз на пружине и R 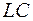-контур.

Пружинный маятник

В этом случае на груз (рис. 2.1) кроме упругой силы и силы трения действует внешняя сила вида (12.1), поэтому на основании второго закона Ньютона можно записать

.

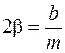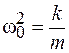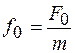Поделив обе части уравнения на и вводя обозначения , , , приведем это уравнение к виду

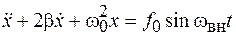. (12.2)

RLC-контур

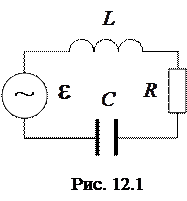
Пусть в колебательном контуре включена ЭДС 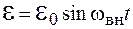, как показано на рисунке 12.1. Тогда по второму закону Кирхгофа для этого контура можно записать

.

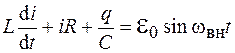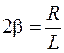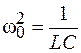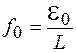Поделив обе части уравнения на индуктивность и вводя обозначения ; ; , с учетом того, что , получим

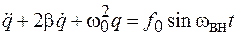. (12.3)

Сравнивая полученное уравнение с уравнением (12.2), видим, что они совпадают с точностью до буквенного обозначения переменной. Отсюда можно сделать вывод, что уравнение (12.2) есть общее дифференциальное уравнение вынужденных колебаний при гармоническом внешнем воздействии на колебательную систему.

Уравнение (12.2) является неоднородным. Из теории дифференциальных уравнений известно, что общее решение неоднородного уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения известно и его можно записать в виде

, (12.4)

где начальная амплитуда 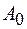и начальная фаза 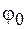определяются начальными условиями.

Частное решение неоднородного уравнения (12.2) будем искать в виде

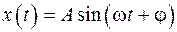, (12.5)

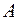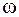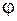где , и соответственно амплитуда, частота и начальная фаза вынужденных колебаний.

Если выражение (12.5) является решением, то при подстановке этого выражения в уравнение (12.2) оно должно обращаться в тождество для любого момента времени. Вычисляя производные и 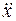, после подстановки их в уравнение (12.2) получим

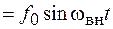. (12.6)

Равенство (12.6) будет выполняться для любого момента времени t, если амплитуда A, частота 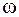и начальная фаза 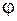удовлетворяют определенным условиям. Чтобы определить эти условия, преобразуем левую часть равенства. Для этого сгруппируем первое и третье слагаемые, а затем воспользуемся известным тригонометрическим равенством

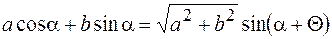, (12.7)

где 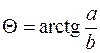. Проделав указанные преобразования, получим

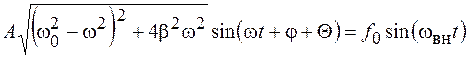, (12.8)

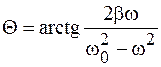. (12.9)

Правая и левая части равенства (12.8) представляют собой гармонические функции, которые будут тождественно равны друг другу, если имеют одинаковую частоту, амплитуду и начальную фазу, т. е.

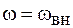, (12.10)

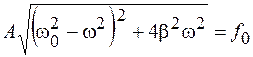, (12.11)

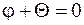. (12.12)

Из (12.10) следует, что частота вынужденных колебаний 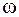равна частоте внешнего воздействия 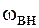. Амплитуду вынужденных колебаний выразим из (12.11):

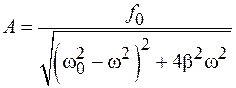, (12.13)

а начальную фазу – из (12.12):

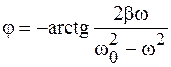. (12.14)

Знак "–" в (12.14) означает, что вынужденные колебания в системе отстают от вынуждающей силы.

Общее решение дифференциального уравнения вынужденных колебаний (12.2) можно записать в виде суммы решений (12.4), (12.5):

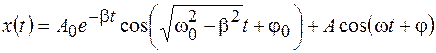, (12.15)

где начальная амплитуда 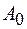и начальная фаза 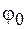определяются начальными условиями, а амплитуда 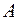и фаза 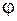– выражениями (12.13), (12.14). Выясним подробнее физический смысл каждого слагаемого в полученном решении.