Комплексная форма представления колебаний
При проведении математических преобразований часто используют комплексную форму представления колебаний. Она основана на известной математической формуле Эйлера:
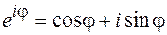 . (8.1)
. (8.1)
В соответствии с формулой Эйлера можно записать
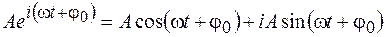 . (8.2)
. (8.2)
Из (8.2) следует, что оба вида гармонических колебаний (3.2) и (3.3) можно представить в виде соответственно действительной и мнимой частей комплексной функции, т. е.

При проведении математических преобразований над функцией  , описывающей колебательный процесс, значки действительной и мнимой частей опускают, а используют саму комплексную функцию
, описывающей колебательный процесс, значки действительной и мнимой частей опускают, а используют саму комплексную функцию 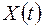 в виде левой части выражения (8.2). Это и есть комплексная форма представления колебаний.
в виде левой части выражения (8.2). Это и есть комплексная форма представления колебаний.
Применение комплексной формы часто оказывается более удобным, так как многие математические преобразования экспоненциальной функции выполняются проще, чем преобразования тригонометрических функций. При этом следует помнить, что реальная физическая величина  (например, смещение груза на пружине, заряд на обкладках конденсатора и т. д.) является действительной и ее представление в виде комплексной функции
(например, смещение груза на пружине, заряд на обкладках конденсатора и т. д.) является действительной и ее представление в виде комплексной функции 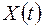 есть лишь удобная математическая форма записи. Поэтому после выполнения математических преобразований для того, чтобы получить реальную физически измеримую величину, следует брать действительную или мнимую часть от полученного результата.
есть лишь удобная математическая форма записи. Поэтому после выполнения математических преобразований для того, чтобы получить реальную физически измеримую величину, следует брать действительную или мнимую часть от полученного результата.
Колебание в комплексной форме можно записать в следующем виде:
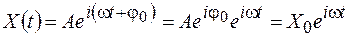 , (8.3)
, (8.3)
где 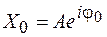 называется комплексной амплитудой колебания.
называется комплексной амплитудой колебания.
Комплексная амплитуда колебания 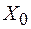 определяет не только максимальное отклонение
определяет не только максимальное отклонение 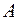 колебательной системы от положения равновесия, но и начальную фазу колебания
колебательной системы от положения равновесия, но и начальную фазу колебания 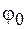 .
.
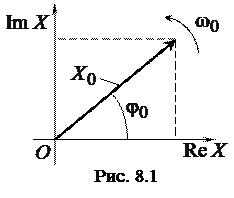 Колебание в комплексной форме графически можно изобразить в виде вектора на комплексной плоскости, модуль которого равен модулю комплексной амплитуды (т. е. амплитуде колебания). Этот вектор образует с действительной осью комплексной плоскости угол
Колебание в комплексной форме графически можно изобразить в виде вектора на комплексной плоскости, модуль которого равен модулю комплексной амплитуды (т. е. амплитуде колебания). Этот вектор образует с действительной осью комплексной плоскости угол 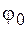 , равный начальной фазе колебания (рис. 8.1). В процессе колебаний вектор вращается вокруг начала координат с угловой скоростью
, равный начальной фазе колебания (рис. 8.1). В процессе колебаний вектор вращается вокруг начала координат с угловой скоростью 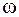 .
.
Дата добавления: 2015-08-08; просмотров: 6204;
