Сложение перпендикулярных колебаний. Фигуры Лиссажу
Если колебательная система имеет две степени свободы, то ее состояние характеризуется двумя независимыми величинами  и
и 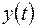 , т. е. некоторой точкой на плоскости
, т. е. некоторой точкой на плоскости 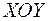 . Так как координаты
. Так как координаты  и
и 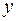 меняются во времени, то точка совершает движение по плоскости
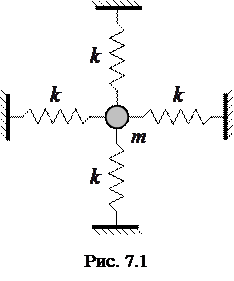
меняются во времени, то точка совершает движение по плоскости 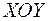 . Простейший пример такой системы приведен на рисунке 7.1. Колебания груза на пружинах могут происходить в двух взаимно перпендикулярных направлениях, поэтому движение груза представляет собой сложение двух перпендикулярных колебаний
. Простейший пример такой системы приведен на рисунке 7.1. Колебания груза на пружинах могут происходить в двух взаимно перпендикулярных направлениях, поэтому движение груза представляет собой сложение двух перпендикулярных колебаний  и
и 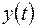 .
.
Рассмотрим случай, когда  и
и 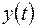 изменяются с одной и той же частотой
изменяются с одной и той же частотой 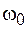 и имеют разность фаз
и имеют разность фаз 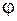 . Если начало отсчета времени выбрать так, чтобы начальная фаза колебания
. Если начало отсчета времени выбрать так, чтобы начальная фаза колебания  равнялась нулю, то складываемые перпендикулярные колебания можно записать в виде
равнялась нулю, то складываемые перпендикулярные колебания можно записать в виде
 (7.1)
(7.1)
 Уравнения (7.1) определяют траекторию движения точки на плоскости
Уравнения (7.1) определяют траекторию движения точки на плоскости 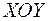 в параметрической форме. Чтобы получить явное выражение
в параметрической форме. Чтобы получить явное выражение 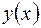 для траектории, необходимо исключить из системы уравнений (7.1) время
для траектории, необходимо исключить из системы уравнений (7.1) время  . Из аналитической геометрии известно, что в общем случае получается уравнение эллипса, у которого размеры полуосей и их наклон по отношению к координатным осям определяются амплитудами
. Из аналитической геометрии известно, что в общем случае получается уравнение эллипса, у которого размеры полуосей и их наклон по отношению к координатным осям определяются амплитудами 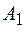 ,
, 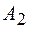 и разностью фаз
и разностью фаз 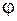 . Рассмотрим некоторые частные случаи:
. Рассмотрим некоторые частные случаи:
а) 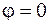 .
.
Используя формулы приведения для тригонометрических функций, легко показать, что 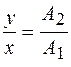 . Отсюда следует, что траектория движения точки представляет собой прямую
. Отсюда следует, что траектория движения точки представляет собой прямую 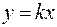 (рис. 7.2, а), проходящую через первый и третий квадранты и образующую с осью
(рис. 7.2, а), проходящую через первый и третий квадранты и образующую с осью 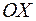 угол
угол 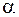 , определяемый соотношением
, определяемый соотношением
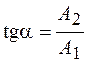 ;
;
б)  .
.
Аналогично предыдущему случаю можно сделать вывод, что траектория движения точки представляет собой прямую 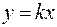 , проходящую через второй и четвертый квадранты (рис. 7.2, б) и образующую с осью
, проходящую через второй и четвертый квадранты (рис. 7.2, б) и образующую с осью 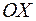 угол
угол 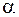 , определяемый соотношением
, определяемый соотношением
 ;
;
в) 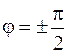 .
.
В этом случае уравнения (7.1) принимают вид

Независимо от знака 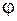 эти уравнения после исключения времени дают уравнение эллипса, полуоси которого совпадают с осями координат:
эти уравнения после исключения времени дают уравнение эллипса, полуоси которого совпадают с осями координат:
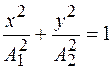 .
.
Если разность фаз 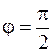 , то движение точки по эллипсу происходит по часовой стрелке (рис. 7.2, в). При
, то движение точки по эллипсу происходит по часовой стрелке (рис. 7.2, в). При 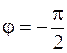 изображающая точка движется против часовой стрелки (рис. 7.2, г).
изображающая точка движется против часовой стрелки (рис. 7.2, г).
Если частоты перпендикулярных колебаний не равны, то результат их сложения не столь однозначен. При произвольном соотношении частот траектория движения изображающей точки не может быть представлена в виде какой-либо замкнутой линии, а будет сплошь заполнять на плоскости 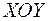 прямоугольник со сторонами
прямоугольник со сторонами 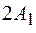 и
и 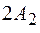 . Движение точки по устойчивой замкнутой траектории будет происходить лишь в том случае, если частоты складываемых колебаний
. Движение точки по устойчивой замкнутой траектории будет происходить лишь в том случае, если частоты складываемых колебаний 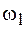 и
и 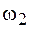 относятся как простые целые числа, т. е.
относятся как простые целые числа, т. е. 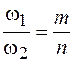 . Получающиеся при этом фигуры называются фигурами Лиссажу.
. Получающиеся при этом фигуры называются фигурами Лиссажу.
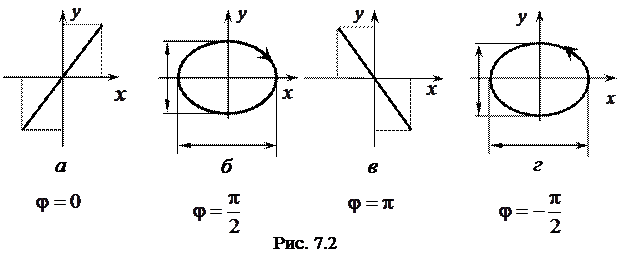 |
 |
Примеры фигур Лиссажу приведены на рисунке 7.3. Каждая фигура вписана в прямоугольник со сторонами
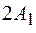 и
и 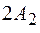 , причем числа касаний фигурой Лиссажу сторон прямоугольника равны
, причем числа касаний фигурой Лиссажу сторон прямоугольника равны  и
и 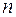 . Фигуры Лиссажу можно наблюдать на экране осциллографа, если на вертикальные и горизонтальные отклоняющие пластины подать напряжения, пропорциональные соответственно
. Фигуры Лиссажу можно наблюдать на экране осциллографа, если на вертикальные и горизонтальные отклоняющие пластины подать напряжения, пропорциональные соответственно  и
и 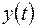 .
.
Форма фигур Лиссажу зависит от разности начальных фаз колебаний. Наблюдение фигур Лиссажу используется для сравнения частот и разности фаз двух гармонических колебаний.
Дата добавления: 2015-08-08; просмотров: 1923;
