Сложение гармонических колебаний одного направления.

Биения

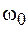Рассмотрим колебательную систему с одной степенью свободы, состояние которой определяется зависимостью некоторой величины от времени. Пусть колебание в этой системе представляет собой сумму двух гармонических колебаний с одинаковой частотой , но различными амплитудами и начальными фазами, т. е.

.

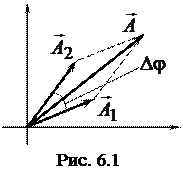Так как "смещение" колебательной системы от положения равновесия происходит вдоль одного единственного "направления" , то в этом случае говорят о сложении гармонических колебаний одного направления. На векторной диаграмме складываемые колебания изобразятся в виде двух векторов и 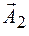, повернутых относительно друг друга на угол 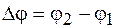(рис. 6.1). Так как частоты складываемых колебаний одинаковы, то их взаимное положение будет оставаться неизменным в любой момент времени, и результирующее колебание будет изображаться вектором, равным сумме векторов и 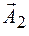. Складывая векторы по правилу параллелограмма и используя теорему косинусов, получим

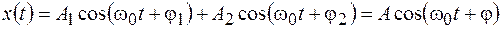, (6.1)

где

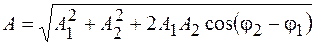, (6.2)

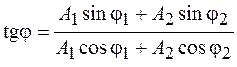. (6.3)

Таким образом, при сложении двух гармонических колебаний одного направления с одинаковыми частотами получается гармоническое колебание той же частоты, амплитуда и начальная фаза которого определяются выражениями (6.2), (6.3).

Два гармонических колебания, которые совершаются с одинаковой частотой и имеют постоянную разность фаз, называются когерентными. Следовательно, при сложении когерентных колебаний получается гармоническое колебание той же частоты, амплитуда и начальная фаза которого определяются амплитудами и начальными фазами складываемых колебаний.

Если складываемые колебания имеют разные частоты и 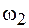, но одинаковые амплитуды 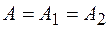, то, используя известное из тригонометрии выражение для суммы косинусов двух углов, получим

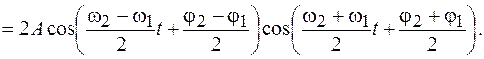(6.4)

Из полученного выражения видно, что результирующее колебание не является гармоническим.

Пусть частоты складываемых колебаний близки друг к другу так, что 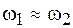и 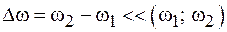. Этот случай называется биением двух частот.

Обозначив 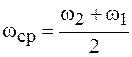, 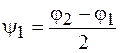и , можно записать

. (6.5)

Из выражения (6.5) следует, что результирующее колебание можно представить как гармоническое колебание с некоторой средней частотой 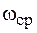, амплитуда которого медленно (с частотой 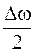) меняется во времени. Время называется периодом биений, а 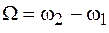– частотой биений. График биений изображен на рисунке 6.2. Биения возникают при 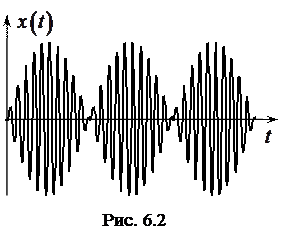одновременном звучании двух камертонов одинаковой тональности. Их можно наблюдать с помощью осциллографа при сложении гармонических колебаний двух генераторов, настроенных на одну частоту. В обоих случаях частоты источников колебаний будут немного различаться, в результате чего возникнут биения.

Так как колебания происходят с разными частотами, то разность фаз складываемых колебаний 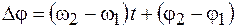изменяется во времени, следовательно, колебания не являются когерентными. Изменение во времени амплитуды результирующих колебаний является характерным следствием некогерентности складываемых колебаний.

Сложение колебаний очень часто наблюдается в электрических цепях и, в частности, в радиотехнических устройствах связи. В одних случаях это делается целенаправленно, чтобы получить сигнал с заданными параметрами. Так, например, в гетеродинном приемнике принимаемый сигнал складывается (смешивается) с сигналом гетеродина, чтобы в результате последующей обработки получить колебание промежуточной частоты. В других случаях сложение колебаний происходит самопроизвольно, когда на вход устройства кроме полезного сигнала поступает какая-либо помеха. По сути, все многообразие формы электрических сигналов представляет собой результат сложения двух или большего числа гармонических колебаний.