Графическое изображение колебаний

Одним из способов графического изображения колебаний является построение графика функции . Однако такой способ не всегда удобен, и часто колебания изображают с помощью векторной диаграммы.

Запишем гармоническое колебание в виде

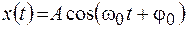. (5.1)

Построим на плоскости 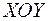(рис. 5.1) вектор длиной 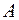, который образует с осью 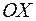угол , причем положительный угол будем откладывать против часовой стрелки. Тогда проекции этого вектора на оси ординат и абсцисс будут соответственно 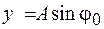и .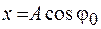

При вращении вектора вокруг начала координат с угловой скоростью 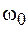его проекции на оси координат будут изменяться по законам 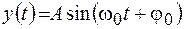и 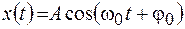. Таким образом, оба вида гармонического колебания (3.2), (3.3) можно представить как изменение проекций на координатные оси некоторого вектора 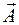, модуль которого равен амплитуде колебания и который вращается со скоростью 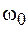, образуя в начальный момент времени 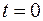угол с осью абсцисс. Такое изображение колебаний называется векторной диаграммой.

Кроме векторной диаграммы для изображения колебаний используется также метод фазовой плоскости. Фазовой плоскостью называется плоскость, на которой координатами являются физическая величина , характеризующая состояние системы, и ее первая производная . Тогда для колебания (5.1) координаты изображающей точки на фазовой плоскости 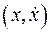представлены в формуле 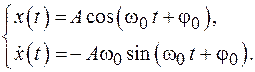(5.2)

(5.2)

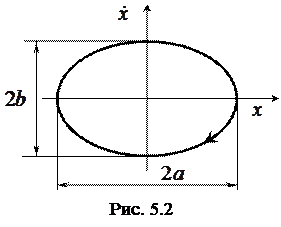
Выражение (5.2) представляет собой параметрическое уравнение эллипса. В процессе колебаний изображающая точка движется на фазовой плоскости по эллипсу с полуосями 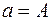; 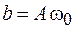по часовой стрелке (рис. 5.2). Изображение колебаний на фазовой плоскости позволяет наглядно представить процессы в системе.