Колебательные контуры. Квазистационарные токи.

Колебания электрических величин — заряда, напряжения, тока — можно наблюдать в цепи, состоящей из последовательно соединённых сопротивления (R), ёмкости (C) и катушки индуктивности (L) (рис. 11.1).

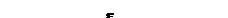
Рис. 11.1.

При положении 1 переключателя К, конденсатор заряжается от источника e.

Если теперь переключить его в положение 2, то в цепи RLC возникнут колебания с периодом T, аналогичные колебаниям груза на пружине.

Колебания, происходящие только за счёт внутренних энергетических ресурсов системы, называются собственными. Первоначально энергия была сообщена конденсатору и локализована в электростатическом поле. При замыкании конденсатора на катушку, в цепи появляется разрядный ток, а в катушке — магнитное поле. Э.д.с. самоиндукции катушки будет препятствовать мгновенной разрядке конденсатора. Через четверть периода конденсатор полностью разрядится, но ток будет продолжать течь, поддерживаемый электродвижущей силой самоиндукции. К моменту 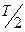эта э.д.с. перезарядит конденсатор. Ток в контуре и магнитное поле уменьшатся до нуля, заряд на обкладках конденсатора достигнет максимального значения.

Эти колебания электрических величин в контуре будут происходить неограниченно долго, если сопротивление контура R = 0. Такой процесс называют собственные незатухающие колебания. Подобные колебания мы наблюдали и в механической колебательной системе, когда в ней отсутствует сила сопротивления. Если сопротивлением резистора R (силой сопротивления в механическом осцилляторе) пренебречь нельзя, то в подобных системах будут происходить собственные затухающие колебания.

На графиках рис. 11.2. представлены зависимости заряда конденсатора от времени в случае незатухающих (а) и затухающих (б, в, г) колебаний. Характер затухающих колебаний меняется с увеличением сопротивления резистора R. Когда сопротивление превысит определённое критическое значение R_к, колебания в системе не возникают. Происходит монотонный апериодический разряд конденсатора (рис. 11.2.г.).

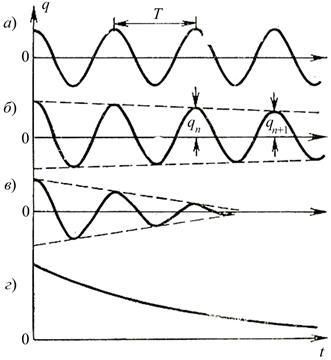
Рис. 11.2.

Прежде, чем перейти к математическому анализу колебательных процессов, сделаем одно важное замечание. При составлении уравнений колебаний мы будем пользоваться правилами Кирхгофа (законами Ома), которые справедливы, строго говоря, для постоянного тока. Но в колебательных системах ток меняется во времени. Однако, и в этом случае можно воспользоваться этими законами для мгновенного значения тока, если скорость изменения тока не слишком высока. Такие токи называются квазистационарными («квази» (лат.) — как будто). Но что значит скорость «слишком» или «не слишком» высока? Если ток изменится на некотором участке цепи, тот импульс этого изменения достигнет самой дальней точки контура спустя время:

.

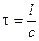Здесь l — характерный размер контура, а с — скорость света, с которой сигнал распространяется в цепи.

Скорость изменения тока считается не слишком высокой, а ток квазистационарным, если:

,

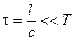где Т — период изменения, тот есть характерное время колебательного процесса.

Например, для цепи длиной 3 м запаздывание сигнала составит t = 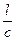= = 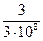10^‑8 с. То есть переменный ток в этой цепи можно считать квазистационарным, если его период более »10^–6 с, что соответствует частоте n = 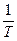£ 10⁶ Гц. Таким образом, для частот 0 £ n £ 10⁶ Гц в рассматриваемой цепи могут быть использованы правила Кирхгофа для мгновенных значений тока и напряжений.