Собственные незатухающие колебания

Такие колебания возникают в электромагнитном колебательном контуре, если его сопротивление R равно нулю (рис. 11.3.).

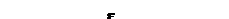
Рис. 11.3.

Сначала зарядим конденсатор С, затем, перекинув ключ К в положение 2, замкнём его на катушку индуктивности L. Начнётся разряд конденсатора. Запишем уравнение правила напряжений Кирхгофа:

–U_C = e^СИ.

Здесь U_C = 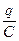— напряжение на конденсаторе; e^СИ = 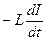= = 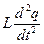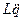— э.д.с. самоиндукции; I = 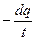= 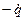— ток в контуре.

Учитывая последние соотношения, перепишем уравнение Кирхгофа в виде:

;

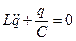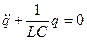. (11.1)

Это линейное дифференциальное уравнение второго порядка — дифференциальное уравнение собственных незатухающих электрических колебаний. Решением этого уравнения является следующая гармоническая функция:

q = Acos(w₀t + j). (11.2)

Проверить это утверждение проще всего методом подстановки:

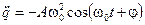. (11.3)

(11.2) и (11.3) подставим в (11.1):

.

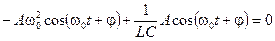Это уравнение становится тождеством, если .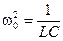

Но w₀ — частота колебаний. Следовательно, частота собственных незатухающих колебаний гармонического осциллятора:

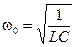. (11.4)

Постоянные А и j в решении (11.2) определяются из начальных условий колебательного процесса. Пусть в момент запуска часов (t = 0) q(0) = q₀, а ток в цепи отсутствует I(0) = 0. Это означает, что (см. 11.2):

q(0) = Acosj = q₀ и

.

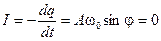Из последнего выражения заключаем, что j = 0, а из предпоследнего, что A = q₀.

Окончательно закон изменения заряда конденсатора во времени (11.2) принимает следующий вид:

q = q₀cos(w₀t).

Ток в цепи при этом меняется так:

. (11.5)

Колебания тока в цепи и заряда конденсатора происходят с одинаковой частотой w₀, но колебания силы тока отстают по фазе на .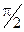

В выражении (11.5) I₀ = q₀w₀ — амплитудное значение силы тока.

Графики зависимостей q = q(t) и I = I(t) приведены на рис. 11.4.

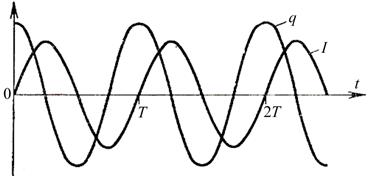
Рис. 11.4.