Формула Гріна

Нехай на області 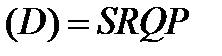, яка є криволінійною трапецією І типа (рис.1), визначена фукнкція 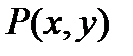, яка є неперервною в 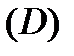разом з частковою похідною 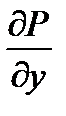. Тоді

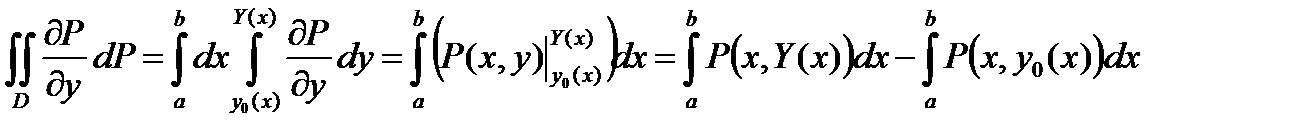. (1)

Але ж

, (2)

Підставимо (2) в (1):

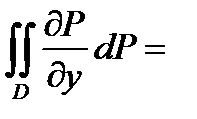
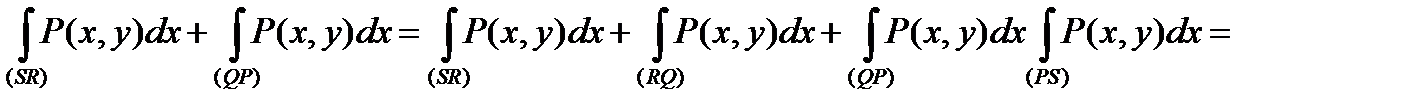
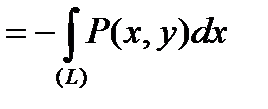, (3)

де 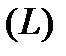- це контур 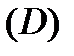, який оббігається в додатному напрямку.

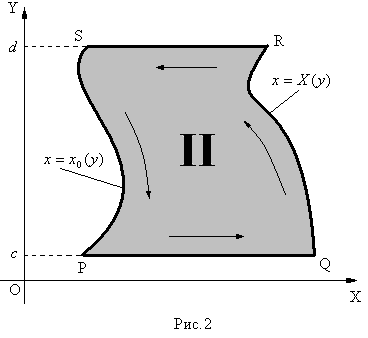
Аналогічно, нехай на області 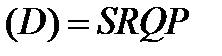, яка тепер є криволінійною трпецією ІІ типа (рис.2), визначена функкція 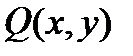, яка є неперервною в 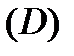разом з частковою похідною 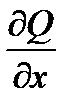. Тоді можна довести, що

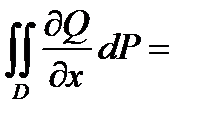
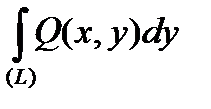. (4)

Зауваження 1. Формула (3) ((4)) має місце, якщо область 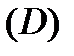прямими, паралельними осі ОУ (осі ОХ) розкладається на скінченну кількість криволінійних трапецій І типу (ІІ типу).

Зауваження 2. Якщо область 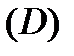одночасно задовольняє умовам обох випадків, тобто розкладається як на скінченну кількість трапецій І типу, так і на скінченну кількість трапецій ІІ типу, і якщо припустити неперервність , , 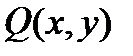, , 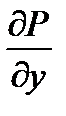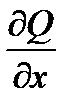то

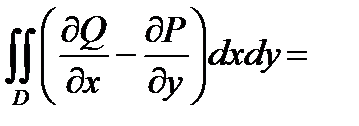
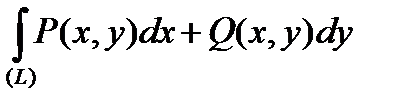. (5)

Формула (5), яка встановлює звязок між криволінійним і подвійним інтегралами, називається формулою Гріна.

Приклад. Перевірити формулу Гріна для функцій 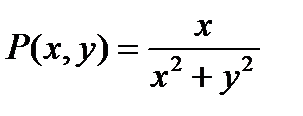, . Обидві функції мають розрив в точці (0,0). Розглянемо як 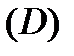коло радиуса 1 з центром в (0,0). Тоді 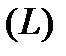визначається як

.

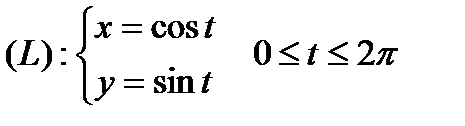При цьому

, ,

.

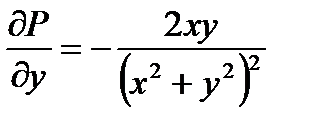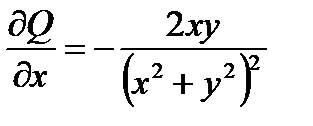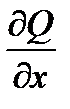
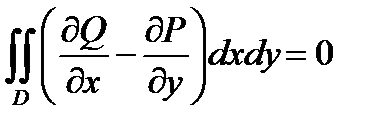Крім того

.

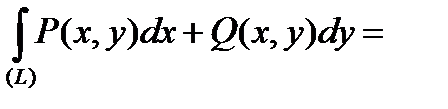
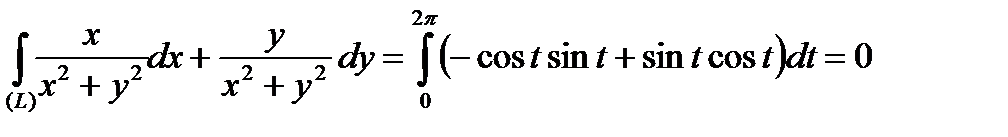Таким чином, формула Гріна має місце, хоча в т.(0,0) функції мають розрив.